Математический маятник

Это материальная точка, подвешенная на невесомой, нерастяжимой нити.

Хорошим приближением к математическому маятнику служит небольшой тяжелый шарик, подвешенный на длинной тонкой нити, рис. 7. Тангенциальное ускорение а, возникает под действием тангенциальной силы 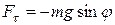. Для малых 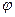можно положить 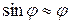и .

Рис. 7

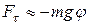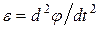С другой стороны тангенциальное ускорение связано с угловым соотношением: .

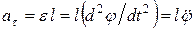Из второго закона Ньютона следует, что 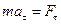, или .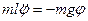

Деля правую и левую части этого уравнения на l, получим:

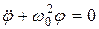, (10)

где 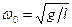. Решением его для малых φ будет:

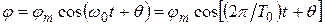, (11)

где

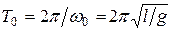. (12)

Таким образом, период колебаний математического маятника T₀, не зависит от его массы и амплитуды колебаний. Измерения T₀ дают возможность с большой точностью определять g , что позволяет проводить гравитометрическую разведку и определять форму фигуры планеты.

Математический маятник сыграл большую роль в открытии закона сохранения энергии и в создании общей теории относительности, основным положением которой является равенство массы гравитационной и инертной.

Пружинный маятник

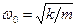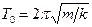Это груз массой т , подвешенный на абсолютно упругой пружине и совершающий колебания около положения равновесия, рис. 1. Он был рассмотрен в параграфе 1. Для него и (13)

7.3. Физический маятник

Рис. 8

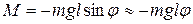Это твердое тело, совершающее колебания под действием силы тяжести вокруг неподвижной горизонтальной оси подвеса, не проходящей через центр масс С тела. На маятник, отклоненный на малый угол φ действует момент силы , который сообщает угловое ускорение 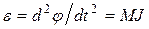, где J - момент инерции тела, относительно оси, проходящей через точку О перпендикулярно рисунку.

С учетом этого получается дифференциальное уравнение . Разделив правую и левую части последнего уравнения на момент инерции тела J, найдем: ,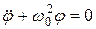

где 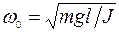. (14)

Решением его будет .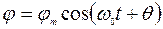

Период колебания 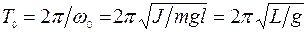, (15)

где L = J/ml - приведенная длина физического маятника; L - это длина такого математического маятника, период колебаний которого совпадает с периодом колебания данного физического маятника.

Точка О' , расположенная на расстоянии L от точки О (рис. 8), через которую проходит ось подвеса физического маятника, называется его центром качаний. Периоды колебаний относительно точек О и О' совпадают.