Основное уравнение релятивистской динамики

Согласно (20), релятивистский импульс 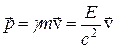, при этом обе формулы справедливы для «тяжелых», т.е. имеющих не нулевую массу частиц. Для безмассовых частиц (т = 0) .

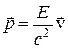Основное уравнение релятивистской динамики имеет вид 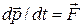или, более подробно:

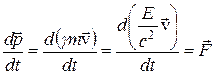. (25)

В силу однородности пространства в релятивистской механике выполняется закон сохранения релятивистского импульса:

релятивистский импульс замкнутой системы сохраняется.

Кинетическая энергия релятивистской частицы

Согласно (19), полная энергия тела (частицы) в релятивистской механике 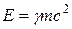, она складывается из энергии покоя тела 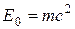[см. (17)] и кинетической энергии 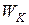, т.е. 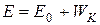, отсюда,

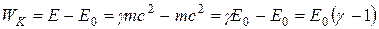. (26)

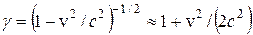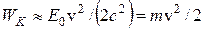Из (26) следует, что при v/c << 1 и , т.е. получаем выражение кинетической энергии частицы, которое используется в ньютоновской механике.

Заметим, что энергия покоящегося тела в ньютоновской механике 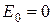, а в релятивистской .

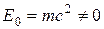В силу однородности времени в релятивистской механике, как и в ньютоновской механике, выполняется закон сохранения энергии:

полная энергия замкнутой системы сохраняется.

Заключение

Итак, длительность события (времени), размеры тела не являются абсолютными величинами, а зависят от скорости тела, т. е. являются относительными. Кроме того масса и энергия оказались связанными друг с другом, хотя они являются качественно различными свойствами материи. Основной вывод теории относительности сводится к тому, что пространство и время взаимосвязаны и образуют единую форму существования материи: пространство-время. Наиболее общая теория пространства-времени называется общей теорией относительности или теорией тяготения, т.к. согласно этой теории свойства пространства-времени в данной области определяются действующими в ней полями тяготения.

В изложенной выше теории действием тяготения Эйнштейн пренебрег. Поэтому она называется частной (или специальной) теорией относительности, т. к. она является частным случаем общей теории относительности, завершенной Эйнштейном позже, в 1915 г.