Гармонические колебания, маятники

Гармоническиминазываются колебания, при которых физическая (или любая другая) величина изменяется с течением времени по синусоидальному (косинусоидальному) закону:

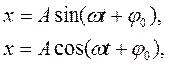(7.1)

где x – значение колеблющейся величины в данный момент времени t (для механических колебаний, например, смещение или скорость, для электрических – напряжение или сила тока); А – амплитуда колебаний; ω - циклическая частота колебаний; (ωt + φ₀) – фаза колебаний; φ₀ – начальная фаза колебаний (рисунок 7.1).

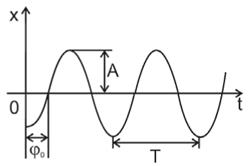
Рисунок 7.1 – Характеристики гармонических колебаний

Этот вид колебаний особенно важен по следующим причинам: во-первых, колебания в природе и в технике часто имеют характер, очень близкий к гармоническим; во-вторых, периодические процессы иной формы (с другой зависимостью от времени) могут быть представлены как наложение нескольких гармонических колебаний.

Время, в течение которого совершается одно колебание, называют периодом колебания – Т(с). Величину, обратную периоду и равную числу колебаний в единицу времени, называют частотой колебания (ν):

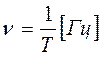, (7.2) причем

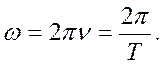(7.3)

Рассмотрим пружинный маятник (рисунок 7.2). При малом смещении шарика вправо относительно положения равновесия на него действует возвращающая сила F – сила упругости, пропорциональная смещению х и направленная к положению равновесия:

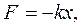(7.4)

где k – коэффициент упругости [Н/м].

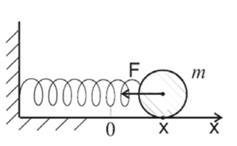
Рисунок 7.2 – Пружинный маятник

Уравнение движения пружинного маятника определяется вторым законом Ньютона: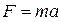

Так как 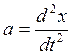, то уравнение движения шарика примет вид

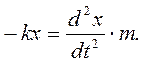(7.5)

Преобразуем это уравнение:

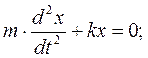
или 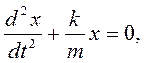(7.6)

где 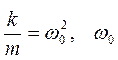- круговая частота собственных колебаний.

Следовательно, период собственных колебаний пружинного маят­ника будет определяться выражением

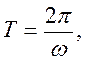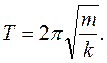или (7.7)

Запишем общий вид дифференциального уравнения гармонических колебаний:

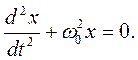(7.8)

Решением этого уравнения является функция 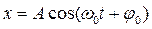, что можно проверить подстановкой.

Математический маятник – материальная точка, подвешенная на растяжимой и невесомой нити (рисунок 7.2).

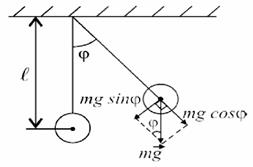
Рисунок 7.2 – Математический маятник

Момент силы, действующей на маятник равен,

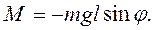(7.9)

Знак «­» указывает, что момент силы противоположен направлению поворота. Так как угол φ мал, то sin φ = φ. Основное уравнение динамики для вращающегося тела имеет вид

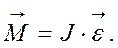(7.10)

Для математического маятника момент инерции 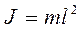, а угловое ускорение 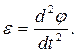Тогда уравнение движения математического маятника запишется в виде:

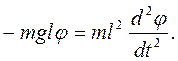(7.11)

Перепишем это уравнение в следующем виде:

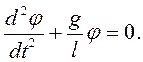(7.12)

Мы получили дифференциальное уравнение второго порядка, решением которого является

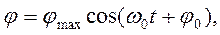
где частота собственных колебаний маятника, 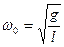т.е. период собственных колебаний равен

(7.13)

Выражение определено только для малых углов φ.

Физический маятник представляет собой твердое тело, совершающее колебания под действием силы тяжести вокруг неподвижной горизонтальной оси, не проходящей через центр масс (центр тяжести) тела (рисунок 7.3).

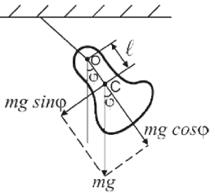
Рисунок 7.3 – Физический маятник

Колебания маятника, как и в случае математического маятника, совершаются под действием силы тяжести:

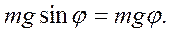(7.14)

Если маятник отклонить на некоторый угол φ от положения равновесия, то на него будет действовать момент силы:

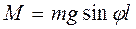(7.15)

(или для малых углов 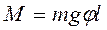), возвращающий его в исходное положение, где l – расстояние от точки подвеса Одо центра тяжести маятника – С.

Воспользовавшись основным уравнением динамики вращательного движения 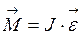запишем уравнение колебаний физического маятника:

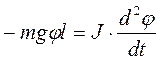или 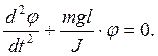(7.16)

Решением этого уравнения является выражение вида

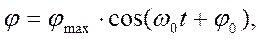
где 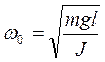частота собственных колебаний маятника.

Таким образом, маятник будет совершать гармонические колебания, период которых определяется выражением

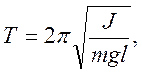(7.17)

где 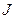– момент инерции маятника относительно оси подвеса; m – масса физического маятника; l – расстояние от точки подвеса до центра тяжести маятника.

Свойствами маятников широко пользуются в различных приборах (в часах, в приборах для определения ускорения свободного падения, ускорений движущихся тел, колебаний земной коры, в гироскопических устройствах, в приборах для экспериментального определения момента инерции тел).

Колебания любых физических величин почти всегда связаны с попеременным превращением энергииодного вида в энергию другого вида.

Так, при отклонении маятника от положения равновесия увеличивается потенциальная энергия груза, запасенная им в поле тяжести; если груз отпустить, он падает, вращаясь около точки подвеса как около центра; в нижнем положении потенциальная энергия превращается в кинетическую, и груз проскакивает это положение равновесия, увеличивая снова потенциальную энергию. Далее процесс перекачки энергии повторяется, пока рассеяние (диссипация) энергии, обусловленное, например, трением, не приводит к полному прекращению колебаний (рисунок 7.4).

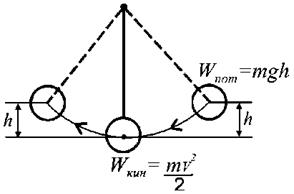
Рисунок 7.4 – Превращение энергии при колебаниях

Полная механическая энергия пружинногомаятника в любой момент времени равна сумме кинетической и потенциальной энергий:

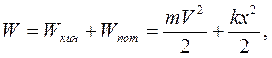(7.18)

где

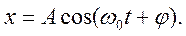
Мгновенная скорость маятника:

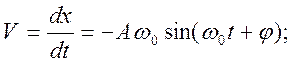
подставив значение V и x в формулу для энергии, получим:

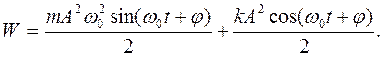
Так как 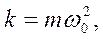то

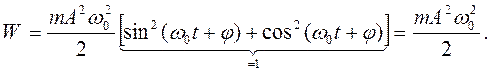(7.19)

Из выражения (7.19) следует, что полная энергия остается постоянной, если рассматриваемая система замкнута (нет рассеяния энергии). Графически зависимость энергии пружинного маятника от смещения х приведена на рисунке 7.5.

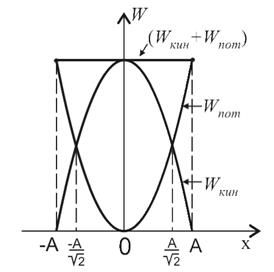
Рисунок 7.5 – зависимость энергии пружинного маятника от смещения