Колебания математического маятника

Рассмотрим в качестве примера колебания математического маятника— материальной точки или грузика, размерами которого можно пренебречь и который подвешен на нерастяжимой невесомой нити. Положение нити вертикально вниз является положением устойчивого равновесия. Если отклонить направление нити от вертикали, то возникнет сила, возвращающая ее в прежнее положение. Попробуем описать движение такого маятника математически.

В качестве обобщенной координаты удобно выбрать угол φотклонения нити от вертикали. Потенциальная энергия тогда определяется выражением

U = mgh = mgl(1 − cos φ). (10.6)

Кинетическая энергия pавна

Т = mυ²/2 = т(lφ’)²/2 = тl² φ’²/2. (10.7)

В результате полная энергия равна

E=тl²φ’²/2 + mgl(1−cosφ). (10.8)

Она остается постоянной в процессе движения. Если мы интересуемся малыми колебаниями φ< 1, то cos φможно разложить в ряд Тейлора:

cosφ = 1-φ²/2!

Тогда

E=тl²φ’²/2 + mglφ²/2=ml²(φ’²+qφ²/l)/2. (10.8а)

Сравнивая это с выражением 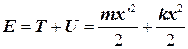(10.3), мы приходим к выводу, что математический маятник колеблется с частотой 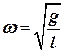, Т 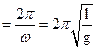. Уравнение колебаний имеет следующий вид, аналогичный (10.4):

φ’’+w²φ = 0. (10.9)

Его можно получить, воспользовавшись, например, законом сохранения энергии. Дифференцируя (10.8а) по времени и приравнивая производную нулю, мы приходим к нужному результату

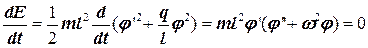(10.10)

Поскольку в общем случае тl²φ’¹ 0, то должно обращаться в нуль выражение в круглых скобках.