Вынужденные колебания

Они возникают при действии на систему внешней периодически изменяющейся силы (вынуждающей силы) 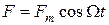, (22)

где 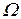- круговая частота вынуждающей силы.

Дифференциальное уравнение вынужденных колебаний с учетом затухания запишется в виде:

m(d²x/dt²) = -kx - r(dx/dt) + F_mcos 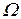t.

Перепишем это уравнение в виде:

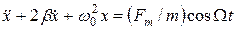. (23)

Таким образом, получили линейное неоднородное дифференциальное уравнение второго порядка с постоянными коэффициентами. Решением такого уравнения будет 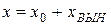, где 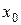– общее решение однородного уравнения (23), (т. е. уравнения (23) с правой частью, равной нулю). Согласно (17)

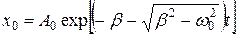
и с течением времени . Поэтому .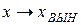

Из решения (23) следует, что 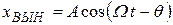(24)

где 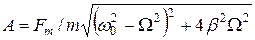, (25)

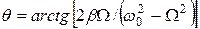. (26)

Из анализа (25) следует, что хотя амплитуда вынуждающей силы F_m, остается постоянной, амплитуда А вынужденных колебаний зависит от частоты 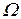вынуждающей силы.

Исследуя (25) на экстремум, можно показать, что только при резонансной частоте

Рис. 11

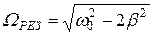(27)

амплитуда вынужденных колебаний достигает максимальной величины: 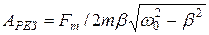. (28)

Это явление называется резонансом.

На рис. 11 приведена зависимость амплитуды А вынужденных колебаний от частоты 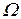вынуждающей силы , которая определяется формулой (25); (откуда: при 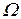= 0 находим 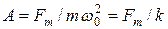, а при 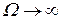имеем 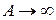, что объясняется инерционностью колебательной системы).

Явление резонанса, состоящее в резком увеличении амплитуды колебаний при приближении частоты вынуждающей силы к резонансной частоте, широко используется в технике. Его следует учитывать при конструировании машин, кораблей, самолетов и т.д. Необходимо, чтобы их резонансные частоты не совпадали с частотой вынуждающих внешних воздействий.

При написании конспекта лекций использовались известные учебники по физике, изданные в период с 1923 г. (Хвольсон О. Д. «Курс физики») до наших дней (Детлаф А. А., Яворский Б. М., Савельев И. В., Сивухин Д. В., Трофимова Т. И., Суханов А. Д. и др.).