Стационарное уравнение Шредингера.

В частном случае, если силовое поле, в котором движется частица, стационарное, то u(x,y,z) имеет смысл потенциальной энергии.

Получим уравнение Шрёдингера для стационарных состояний .В этом случае решение уравнения Шрёдингера распадается на 2 множителя, один из которых зависит только от координат, другой только от времени.

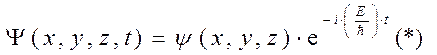
Здесь E – полная энергия частицы, которая в следующем стационарном поле остаётся const.

Подставим (**) в (*) , получим :

(**)

Сократить на множитель 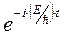, получим стационарное уравнение Шрёдингера

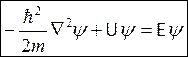
Функции ψ, удовлетворяющие уравнению Шредингера при заданной U, называются собственными функциями.

В теории дифференциальных уравнений доказывается, что уравнения вида уравнения Шредингера имеют решения не при любых значениях Е, а лишь при некоторых. Значения, при которых существуют решения, называются собственными значениями.Физический смысл величины Е – полная энергия частицы.

Совокупность собственных значений называется спектром величины. Если эта совокупность образует дискретную последовательность, спектр называется дискретным. Если собственные значения образуют непрерывную последовательность, то спектр называют непрерывным или сплошным. Величина, имеющая дискретный спектр, называется квантованной.

В случае дискретного спектра собственные значения и собственные функции можно пронумеровать

Если одному собственному значению соответствует несколько собственных функций

,

то состояние с энергией Е_i называют вырожденным, k – кратность вырождения. В противном случае состояние называют невырожденным.

Уравнение Шредингера позволяет найти пси-функцию данного состояния и, следовательно, определить вероятность нахождения частицы в различных точках пространства. Для этого надо:

1) записать уравнение Шредингера с учетом конкретного вида потенциальной энергии;

2) решить уравнение Шредингера, т.е. найти собственные функции и собственные значения, удовлетворяющие начальным и граничным условиям.

Далее будем заниматься отысканием собственных функций и собственных значений для некоторых конкретных задач. Нахождение собственных значений и собственных функций, как правило, представляет весьма трудную математическую задачу. Прежде чем рассматривать конкретные задачи атомной физики, решим простейшие модельные задачи.