Соотношение неопределенностей.

Корпускулярно-волновая двойственность свойств микрочастиц приводит к вопросу о границе применимости понятий классической физики в микромире. В классической механике состояние материальной точки (классической частицы) определяется заданием значений координат, импульса и энергии. В квантовой механике в 1927 г. Гейзенберг установил основополагающий принцип, который называют принципом неопределенностей. Количественные соотношения, выражающие этот принцип в конкретных случаях, называют соотношениями неопределенностей. Согласно Гейзенбергу, микрочастица не может одновременно иметь точно определенную координату и соответствующую компоненту импульса

.

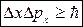Здесь Δx – неопределенность координаты частицы, Δp_x - неопределенность импульса частицы. Из соотношения следует, что если Δx = 0, т.е. координата определена точно, то импульс частицы совершенно не определен

.

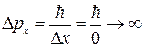Аналогичные соотношения можно записать для других компонент

.

Другими словами, классические понятия координаты и импульса применимы к микрочастицам лишь в пределах, устанавливаемых соотношениями Гейзенберга.

Для энергии и времени справедливо соотношение неопределенностей

.

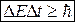Рассмотрим следующий мысленный эксперимент. Попытаемся определить значение координаты x свободно летящей микрочастицы, поставив на ее пути щель ширины Δx, расположенную перпендикулярно к направлению движения частицы.

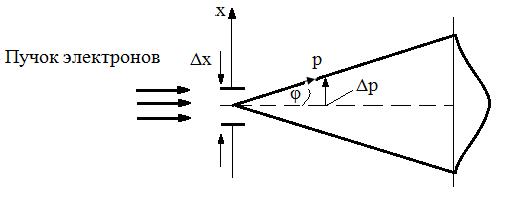
До прохождения частицы через щель ее составляющая импульса имеет точное значение p_x = 0, зато координата x частицы не определена и Δx = ∞. В момент прохождения частицы через щель неопределенность координаты равна ширине щели, но исчезает определенность импульса

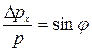
Вследствие дифракции имеется некоторая вероятность того, что частица будет двигаться в пределах угла 2φ, где φ – угол соответствующий первому дифракционному минимуму. Условие первого дифракционного минимума при дифракции на одной щели ширины Δx

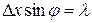
Отсюда

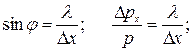
Так как 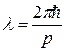, то

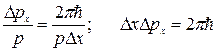
Эти рассуждения нельзя рассматривать как строгий вывод, но по порядку величины мы получили верное соотношение.

Соотношение неопределенности показывает, что определить положение частицы в пространстве и направление ее скорости нельзя одновременно точно, поэтому к микрочастице нельзя применять понятие траектории, но с увеличением массы частицы ограничения на возможность применения классических понятий уменьшаются.

С точностью до коэффициента 2π

,

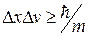то есть чем больше масса частицы, тем меньше неопределенности ее координаты и скорости, следовательно, с тем большей точностью применимо понятие траектории.

Соотношение неопределенности позволяет объяснить тот факт, почему электрон не может упасть на ядро. Если бы электрон упал на ядро, его координаты и импульс приняли бы определенные (нулевые значения), что несовместимо с принципом неопределенности.

С помощью соотношения неопределенностей можно оценить размеры простейшего атома и минимальную энергию электрона в таком атоме.

Энергия электрона в атоме водорода равна

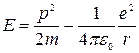
Подведем некоторые приближенные оценки. Полагая 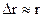и , получим соотношение 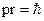. Тогда

.

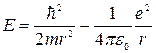Найдем значение r, при котором энергия Е минимальна, продифференцировав по r и приравняв производную нулю

.

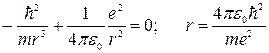Полученное выражение совпадает с радиусом первой боровской орбиты. Подстановка в формулу для энергии дает энергию основного состояния атома водорода

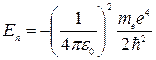
Вопросы для самоконтроля:

1. В чем смысл длины волны де Бройля?

2. Что показал опыт Дэвиссона и Джермера? Фабриканта, Бибермана и Сушкина?

3. В чем смысл соотношений неопределенностей Гейзенберга?

4. Как объяснить наличие естественной ширины (∆ω) спектральных линий исходя из соотношения неопределенностей?

Лекция 5.