Уравнения касательной и нормали к плоской кривой

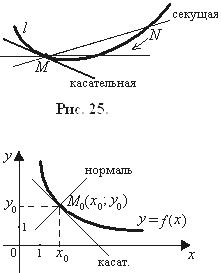Касательной к кривой l в ее точке М называют предельное положение секущей MN, когда точка N, двигаясь по кривой l, неограниченно приближается к точке М (рис. 25).

Нормалью к кривой называется прямая, перпендикулярная касательной к этой кривой и проходящая через точку касания (рис. 26).

Рис. 25

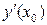Геометрический смысл производной: – это угловой коэффициент касательной к графику 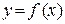в точке 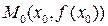: 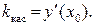Тогда из условия перпендикулярности прямых можно найти угловой коэффициент нормали:

Рис. 26

.

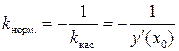Если 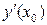существует, то уравнение касательной имеет вид:

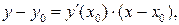(23)

где .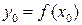

Если 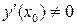, то уравнение нормали имеет вид:

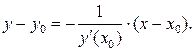(24)

Вычисление пределов при помощи правила Лопиталя

Правило Лопиталя: предел отношения двух бесконечно малых или бесконечно больших функций при x ® a равен пределу отношения их производных, если предел отношения производных существует (конечный или бесконечный):

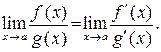(25)

Правило Лопиталя позволяет раскрывать неопределенности вида 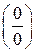или .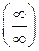

Правило Лопиталя справедливо и в случае, когда x ® ¥. Его можно применять неоднократно.