Предел функции. Предел последовательности
Пусть функция 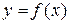 определена в некоторой окрестности точки х = а, где а – конечная или бесконечно удаленная точка на числовой
определена в некоторой окрестности точки х = а, где а – конечная или бесконечно удаленная точка на числовой
прямой Ох.
Число А называется конечным пределом функции 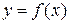 в точке х = а (или при
в точке х = а (или при 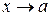 ), если для любого числа
), если для любого числа 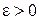 , сколь малым бы оно ни было, можно указать такую окрестность U(a) точки х = а (не включающую саму точку а), что при всех х, принадлежащих этой окрестности, выполняется неравенство
, сколь малым бы оно ни было, можно указать такую окрестность U(a) точки х = а (не включающую саму точку а), что при всех х, принадлежащих этой окрестности, выполняется неравенство 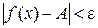 .
.
Предел функции обозначается так: 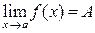 , или
, или 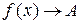 при
при 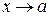 .
.
Определение конечного предела при 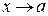 можно записать символически следующим образом:
можно записать символически следующим образом:
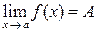
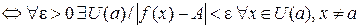 . (*)
. (*)
Геометрически существование конечного предела 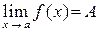 в случае, когда
в случае, когда 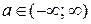 , означает, что значения функции
, означает, что значения функции 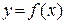 сколь угодно мало отличаются от числа А, если значения аргумента становятся достаточно близкими к точке
сколь угодно мало отличаются от числа А, если значения аргумента становятся достаточно близкими к точке 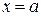 (рис. 1). При этом в самой точке а функцияможет быть не определена или определена, но может иметь значение, отличное от А.
(рис. 1). При этом в самой точке а функцияможет быть не определена или определена, но может иметь значение, отличное от А.
Поведение функции только слева или только справа от точки 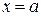 , т. е. в ее левой или правой окрестности, характеризуется ее односторонними пределами (рис. 2): левосторонний предел функции обозначается
, т. е. в ее левой или правой окрестности, характеризуется ее односторонними пределами (рис. 2): левосторонний предел функции обозначается 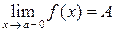 , где условие
, где условие 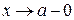 означет, что х остается левее точки а (
означет, что х остается левее точки а ( 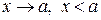 ); правосторонний предел функции обозначается
); правосторонний предел функции обозначается 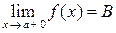 , где условие
, где условие 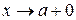 означет, что х остается правее точки а (x ® a, x > a).
означет, что х остается правее точки а (x ® a, x > a).
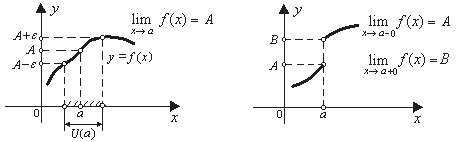
Рис. 1 Рис. 2
Существование предела 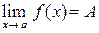 означает, что существуют оба односторонних предела и они совпадают между собой:
означает, что существуют оба односторонних предела и они совпадают между собой:
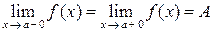 .
.
Если существует конечный предел функции при 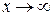 :
: 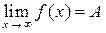 , то в его определении (*) U(a) – это окрестность бесконечно удаленной точки числовой прямой (рис. 3). При этом можно рассматривать односторонние пределы:
, то в его определении (*) U(a) – это окрестность бесконечно удаленной точки числовой прямой (рис. 3). При этом можно рассматривать односторонние пределы: 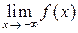 или
или 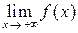 (рис. 4).
(рис. 4).
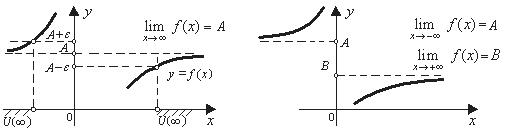
Рис. 3 Рис. 4
Числовую последовательность 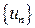 обычно рассматривают как функцию натурального аргумента n:
обычно рассматривают как функцию натурального аргумента n: 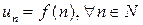 .
.
Если существует предел последовательности 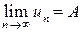 , то его определение можно записать символически:
, то его определение можно записать символически:
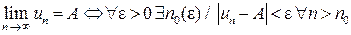 ,
,
т. е. члены последовательности 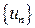 сколь угодно мало отличаются
сколь угодно мало отличаются
от числа А при достаточно больших номерах n (для n > n0).
3. Бесконечно малые, бесконечно большие
и локально ограниченные функции
Функция 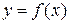 называется бесконечно малой при
называется бесконечно малой при 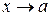 , если
, если 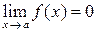 (рис. 5, 6).
(рис. 5, 6).
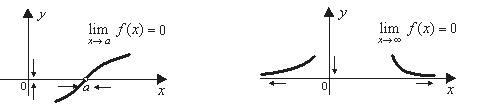
Рис. 5 Рис. 6
Пример: 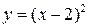 – бесконечно малая функция при
– бесконечно малая функция при 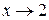 .
.
Две бесконечно малые при 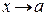 функции f (x) и g (x) называются эквивалентными бесконечно малыми, если
функции f (x) и g (x) называются эквивалентными бесконечно малыми, если 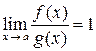 .
.
Основные соотношения эквивалентностей:
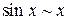 при
при 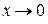 , (1)
, (1)
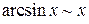 при
при 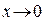 , (2)
, (2)
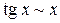 при
при 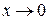 , (3)
, (3)
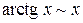 при
при 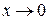 , (4)
, (4)
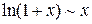 при
при 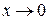 , (5)
, (5)
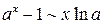 при
при 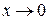 , (6)
, (6)
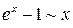 при
при 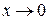 . (7)
. (7)
Функция 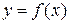 называется бесконечно большой при
называется бесконечно большой при 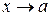 , если для любого числа
, если для любого числа 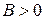 , сколь бы большим оно ни было, можно указать такую окрестность U(a) точки х = а (не включающую саму точку а), что при всех х, принадлежащих этой окрестности, выполняется неравенство
, сколь бы большим оно ни было, можно указать такую окрестность U(a) точки х = а (не включающую саму точку а), что при всех х, принадлежащих этой окрестности, выполняется неравенство 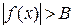 .
.
Предел бесконечно большой функции при 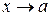 обозначается симво-лом ¥:
обозначается симво-лом ¥: 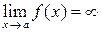 и называется бесконечным пределом функции при x ® a.
и называется бесконечным пределом функции при x ® a.
Определение бесконечно большой функции при x ® a можно записать символически следующим образом:
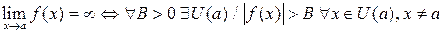 .
.
Геометрически существование бесконечного предела 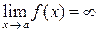
означает, что значения функции 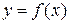 становятся сколь угодно большими по модулю, если значения аргумента достаточно близки к точке х = а (рис. 7, 8).
становятся сколь угодно большими по модулю, если значения аргумента достаточно близки к точке х = а (рис. 7, 8).
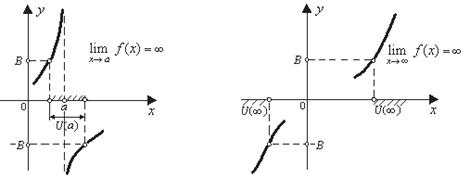
Рис. 7 Рис. 8
Пример. 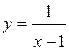 – бесконечно большая функция при x ® 1.
– бесконечно большая функция при x ® 1.
Бесконечный предел последовательности 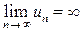 означает, что члены последовательности
означает, что члены последовательности 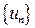 становятся сколь угодно большими по модулю при достаточно больших номерах n:
становятся сколь угодно большими по модулю при достаточно больших номерах n:
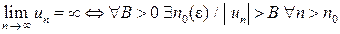 .
.
Функция 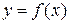 называется локально ограниченной в точке х = а, если существует такая окрестность точки U(a), в которой значения функции удовлетворяют неравенству
называется локально ограниченной в точке х = а, если существует такая окрестность точки U(a), в которой значения функции удовлетворяют неравенству 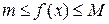 , где m и M – некоторые числа.
, где m и M – некоторые числа.
Любая функция, имеющая конечный предел при x ® a, в том числе
и бесконечно малая функция, является локально ограниченной в точке х = а.
Если 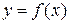 – бесконечно большая при x ® a, то она не является локально ограниченной в точке х = а.
– бесконечно большая при x ® a, то она не является локально ограниченной в точке х = а.
Пример. 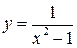 – локально ограниченная функция во всех точках, кроме точек х = 1 и х = –1.
– локально ограниченная функция во всех точках, кроме точек х = 1 и х = –1.
Дата добавления: 2019-05-21; просмотров: 653;











