Исследование функций и построение графиков
Полное исследование функции 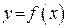 для построения ее графика включает следующие пункты (не обязательно именно в этом порядке).
для построения ее графика включает следующие пункты (не обязательно именно в этом порядке).
1) Область определения функции (ООФ) и область ее значений (ОЗФ)
Если область определения функции 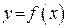 не задана специально,
не задана специально,
то считают, что она совпадает с областью допустимых значений ее аргумента, т. е. с множеством всех точек х, для которых выполнима операция f. При нахождении ООФ используют ООФ элементарных функций 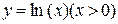 ,
, 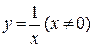 ,
, 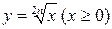 , и др.
, и др.
Область значений функции находят только в случаях, когда ее можно сразу указать, опираясь на свойства элементарных функций, например, для функции 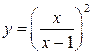 , очевидно,
, очевидно, 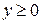 .
.
2) Четность функции, ее периодичность
Для установления четности (нечетности) функции 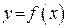 , имеющей симметричную область определения, проверяют справедливость равенств
, имеющей симметричную область определения, проверяют справедливость равенств 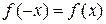 (
( 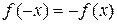 ) для всех x Î ООФ.
) для всех x Î ООФ.
В случае четности или нечетности функции исследование ее поведения и построение графика можно проводить только для 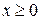 , а затем достроить график, используя симметрию: для четной функции график симметричен относительно оси OY, а для нечетной – относительно начала координат.
, а затем достроить график, используя симметрию: для четной функции график симметричен относительно оси OY, а для нечетной – относительно начала координат.
Для установления периодичности функции проверяют справедливость равенства 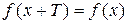 для
для 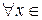 ООФ, где Т определяется видом функции. В случае периодической функции исследование проводят для одного промежутка периодичности.
ООФ, где Т определяется видом функции. В случае периодической функции исследование проводят для одного промежутка периодичности.
3) Непрерывность функции, точки разрыва, вертикальные асимптоты
Для определения промежутков непрерывности функции используют непрерывность основных элементарных функций. В точках, "подозритель-ных" на разрыв (отдельных точек, не входящих в ООФ), проверяют выпол-нение условий непрерывности. Если функция терпит разрыв в точке х0,
то определют тип разрыва.
Если функция 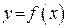 имеет бесконечный разрыв в некоторой точке х0, то прямая х = х0 является вертикальной асимптотой графика функции. Если только один из односторонних пределов при
имеет бесконечный разрыв в некоторой точке х0, то прямая х = х0 является вертикальной асимптотой графика функции. Если только один из односторонних пределов при 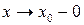 или
или 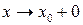 является бесконечным, то асимптота называется односторонней.
является бесконечным, то асимптота называется односторонней.
Если функция определена не на всей числовой оси, то необходимо вычислить односторонние пределы функции в точках, ограничивающих промежутки ООФ. Если односторонний предел функции в точке а, ограни-чивающей промежуток ООФ, бесконечен, то х = а является односторонней вертикальной асимптотой графика функции. Например, если ООФ: 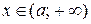 , то нужно найти
, то нужно найти 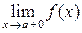 ; если этот предел окажется бесконечным, то х = а является односторонней вертикальной асимптотой графика функции.
; если этот предел окажется бесконечным, то х = а является односторонней вертикальной асимптотой графика функции.
4) Промежутки монотонности и экстремумы
Для определения промежутков монотонности функции 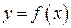
используют достаточный признак монотонности.
Достаточный признак монотонности дифференцируемой функции:
если на интервале х Î (а, b) производная 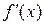 сохраняет знак,
сохраняет знак,
то функция 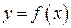 сохраняет монотонность на этом интервале, а именно: если
сохраняет монотонность на этом интервале, а именно: если 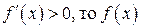 возрастает, если
возрастает, если 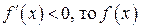 убывает.
убывает.
Для установления точек экстремумов функции 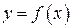 используют необходимый и достаточные признаки существования экстремума.
используют необходимый и достаточные признаки существования экстремума.
Необходимое условие существования экстремума функции: если непрерывная функция 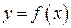 имеет экстремум в точке х0, то ее производная в этой точке равна нулю или не существует.
имеет экстремум в точке х0, то ее производная в этой точке равна нулю или не существует.
Точки, принадлежащие ООФ, в которых производная 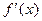 равна нулю или не существует, называют критическими точками функции по ее первой производной (точками, "подозрительными на экстремум").
равна нулю или не существует, называют критическими точками функции по ее первой производной (точками, "подозрительными на экстремум").
Первый достаточный признак существования экстремума: если при переходе через критическую точку х0 (слева направо) производная 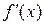 изменяет свой знак, то в точке х0 есть экстремум причем это максимум, если знак
изменяет свой знак, то в точке х0 есть экстремум причем это максимум, если знак 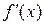 меняется с плюса на минус, и это минимум, если знак
меняется с плюса на минус, и это минимум, если знак 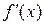 меняется с минуса на плюс. Если при переходе через критическую точку х0 производная
меняется с минуса на плюс. Если при переходе через критическую точку х0 производная 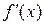 не изменяет свой знак, то в точке х0 нет экстремума функции
не изменяет свой знак, то в точке х0 нет экстремума функции 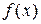 .
.
Второй достаточный признак существования экстремума: если 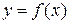 – дважды дифференцируемая функция в точке х0 и
– дважды дифференцируемая функция в точке х0 и 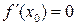 ,
,
тогда: если 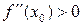 , то х0 – точка минимума функции, а если
, то х0 – точка минимума функции, а если 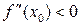 , то х0 – точка максимума.
, то х0 – точка максимума.
Для нахождения точек экстремумов функции 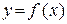 сначала находят критические точки по первой производной. После этого проверяют выполнение в них достаточных условий существования экстремума функции.
сначала находят критические точки по первой производной. После этого проверяют выполнение в них достаточных условий существования экстремума функции.
5) Промежутки выпуклости, вогнутости графика и точки перегиба
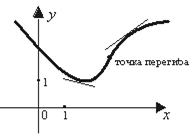 Дуга кривой L называется выпуклой, если все ее точки расположены не выше касательной, проведенной в любой точке этой дуги (рис. 27),
Дуга кривой L называется выпуклой, если все ее точки расположены не выше касательной, проведенной в любой точке этой дуги (рис. 27),
и называется вогнутой, если все ее точки расположены не ниже касательной, проведенной в любой точке дуги кривой.
Рис. 27 Точки, принадлежащие кривой, и отделяющие участки выпуклости от участков вогнутости, называются точками перегиба кривой (рис. 27).
Достаточное условие выпуклости, вогнутости графика функции:если функция 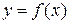 является дважды дифференцируемой и ее вторая производная
является дважды дифференцируемой и ее вторая производная 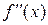 сохраняет знак при всех x Î (a; b), то график функции имеет постоянное направление выпуклости на этом интервале: при
сохраняет знак при всех x Î (a; b), то график функции имеет постоянное направление выпуклости на этом интервале: при 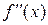 < 0 – выпуклость вверх, при
< 0 – выпуклость вверх, при 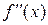 > 0 – вогнутость (выпуклость вниз).
> 0 – вогнутость (выпуклость вниз).
Необходимое условие для точки перегиба: если х0 – абсцисса точки перегиба графика функции 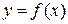 , то ее вторая производная в этой точке равна нулю или не существует.
, то ее вторая производная в этой точке равна нулю или не существует.
Точки, принадлежащие графику функции 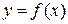 , в которых
, в которых 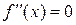 или
или 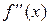 не существует, называются критическими точками функции
не существует, называются критическими точками функции
по ее второй производной (точками, "подозрительными на перегиб").
Достаточное условие для точек перегиба: если вторая производная 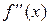 при переходе через точку х0, подозрительную на перегиб, изменяет знак, то точка графика с абсциссой х0 является точкой перегиба. Если
при переходе через точку х0, подозрительную на перегиб, изменяет знак, то точка графика с абсциссой х0 является точкой перегиба. Если 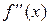 не изменяет знак при переходе через точку х0, то перегиба нет.
не изменяет знак при переходе через точку х0, то перегиба нет.
При нахождении промежутков выпуклости, вогнутости графика функции 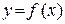 сначала находят критические точки по второй производной, после этого выделяют промежутки знакопостоянства второй
сначала находят критические точки по второй производной, после этого выделяют промежутки знакопостоянства второй
производной на ООФ: если 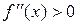 , то кривая вогнутая, а если
, то кривая вогнутая, а если 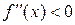 , то кривая выпуклая. Точки перегиба определяют, используя достаточные условия перегиба.
, то кривая выпуклая. Точки перегиба определяют, используя достаточные условия перегиба.
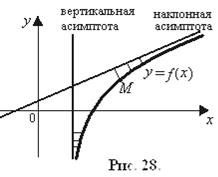 6) Наклонные и горизонтальные асимптоты
6) Наклонные и горизонтальные асимптоты
|
до которой от текущей точки М кривой стремится к нулю при удалении точки М от начала координат (рис. 28).
Если график функции 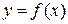 имеет наклонную асимптоту с уравнением
имеет наклонную асимптоту с уравнением 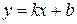 , то параметры k и b в уравнении асимптоты можно найти по формулам:
, то параметры k и b в уравнении асимптоты можно найти по формулам:
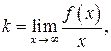 (26)
(26)
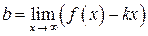 . (27)
. (27)
Если хотя бы один из этих пределов является бесконечным или
не существует, то наклонных асимптот нет. В случае, когда k = 0, график имеет горизонтальную асимптоту с уравнением y = b.
В некоторых случаях (как правило, если f (x) выражена через показательную или логарифмическую функцию), график может иметь асимптоты только при 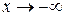 или только при
или только при 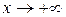 .
.
Иногда ветви графика 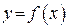 при
при 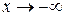 и при
и при 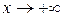 имеют
имеют
разные асимптоты.
7) Точки пересечения графика с осями координат или другие
дополнительные точки графика
Дополнительные точки графика находят в случаях, когда недостаточно информации для выбора масштаба по осям координат, т. е. когда на некотором промежутке ООФ нет ни точек экстремумов, ни точек перегибов,
ни точек пересечения графика с осями координат.
Примерный вариант и образец выполнения контрольной работы 4
Задача 1. Найти производную 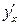 :
:
а) 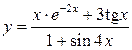 ; б)
; б) 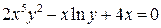 ; в)
; в) 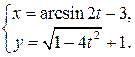
Задача 2. Дана функция 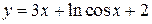 и значение х0 = 0. Найти уравнения касательной и нормали к графику функции в точке с абсциссой х0. Построить графики функции, касательной и нормали в окрестности точки (х0, f (х0)).
и значение х0 = 0. Найти уравнения касательной и нормали к графику функции в точке с абсциссой х0. Построить графики функции, касательной и нормали в окрестности точки (х0, f (х0)).
Задача 3. Вычислить пределы, используя правило Лопиталя:
а) 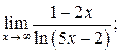 б)
б) 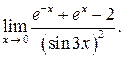
Задача 4. Провести полное исследование функции и построить ее график:
а) 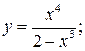 б)
б) 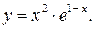
Решение задачи 1а
Функция у(х) задана в явном виде и является отношением двух функций: 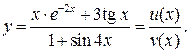 Будем искать ее производную по формуле (20):
Будем искать ее производную по формуле (20):
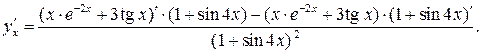
Найдем производные ее числителя и знаменателя:
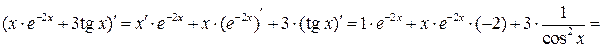
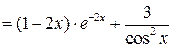
(здесь использованы формулы (18), (19), (21) и "правило цепочки");
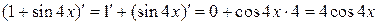
(здесь использованы формулы (17), (18) и "правило цепочки").
Теперь получаем:
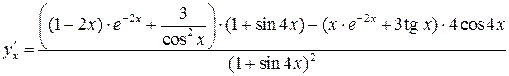 .
.
Преобразование результата не производим, поскольку оно не дает существенного упрощения выражения для 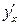 .
.
Решение задачи 1б
Равенство 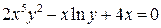 есть уравнение вида
есть уравнение вида 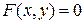 , которое неявно задает функцию
, которое неявно задает функцию 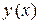 . Для нахождения
. Для нахождения 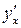 продифференцируем обе части тождества
продифференцируем обе части тождества 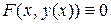 по аргументу х и из полученного равенства найдем
по аргументу х и из полученного равенства найдем 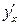 как решение линейного уравнения:
как решение линейного уравнения:
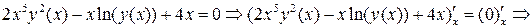
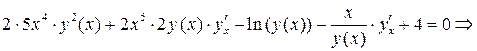
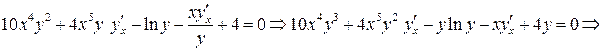
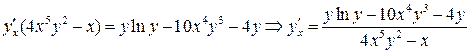 .
.
Производная неявно заданной функции 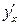 зависит от аргумента х
зависит от аргумента х
и функции у, поэтому в ответе нужно отразить их взаимосвязь:
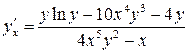 , где
, где 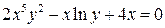 .
.
Решение задачи 1в
Функция у(х) задана параметрически: 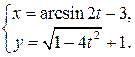 Для нахож-дения
Для нахож-дения 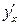 используем формулу (22):
используем формулу (22):
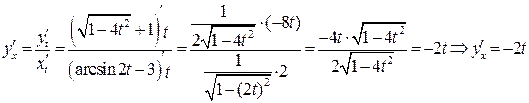
(при дифференцировании использованы формулы (17), (18) и "правило
цепочки").
Производная параметрически заданной функции также является функцией, заданной параметрически, поэтому записываем результат в параметрической форме: 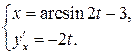
Ответы:
а) 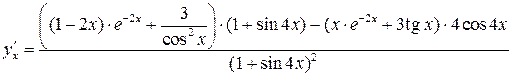 ;
;
б) 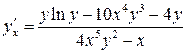 , где
, где 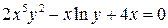 ;
;
в) 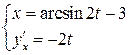 .
.
Решение задачи 2
Найдем ординату точки касания: 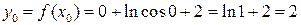 .
.
Для вычисления угловых коэффициентов касательной и нормали
найдем производную 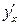 :
:
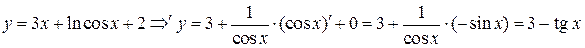 .
.
Вычислим угловой коэффициент касательной: 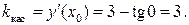 Тогда угловой коэффициент нормали:
Тогда угловой коэффициент нормали: 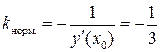 .
.
Запишем уравнение касательной в точке М(0; 2) по формуле (23)
и приведем его к виду общего уравнения прямой:
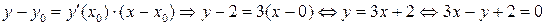 .
.
Запишем уравнение нормали по формуле (24) и аналогично упростим его:
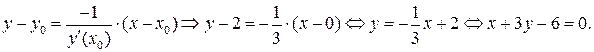
 Для построения графика функции
Для построения графика функции 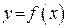 в окрестности точки (х0; у0) вычислим значения функции
в окрестности точки (х0; у0) вычислим значения функции 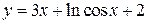 в точках, близких к х0 = 0:
в точках, близких к х0 = 0:
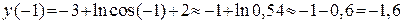 ,
,
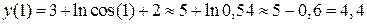 .
.
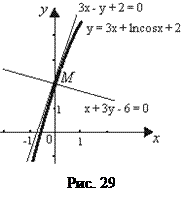
На рис. 29 построены участок графика функции 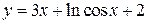 , касательная
, касательная 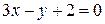 и нор-маль
и нор-маль 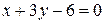 в окрестности точки М(0; 2).
в окрестности точки М(0; 2).
Ответы: 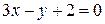 и
и 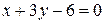 . Графики на рис. 29.
. Графики на рис. 29.
Решение задачи 3а
В данном пределе функция 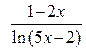 при
при 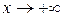 есть отношение двух бесконечно больших функций, т. е. при вычислении предела нужно устранить неопределенность вида
есть отношение двух бесконечно больших функций, т. е. при вычислении предела нужно устранить неопределенность вида 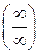 . Используем правило Лопиталя (формула (25)):
. Используем правило Лопиталя (формула (25)):
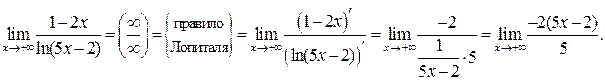
Последний предел есть предел бесконечно большой функции, т. е.
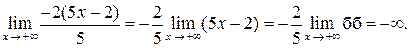
Следовательно, исходный предел 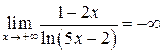 .
.
Решение задачи 3б
В данном пределе функция 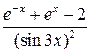 при
при 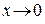 есть отношение двух бесконечно малых функций, т. е. при вычислении предела нужно устранить неопределенность вида
есть отношение двух бесконечно малых функций, т. е. при вычислении предела нужно устранить неопределенность вида 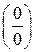 . Используем правило Лопиталя:
. Используем правило Лопиталя:
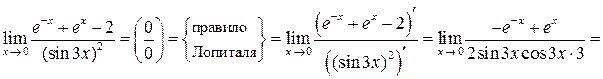
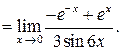
Последний предел при 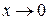 есть отношение двух бесконечно малых функций, т. е. нужно снова устранять неопределенность вида
есть отношение двух бесконечно малых функций, т. е. нужно снова устранять неопределенность вида 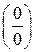 . Еще раз используем правило Лопиталя:
. Еще раз используем правило Лопиталя:
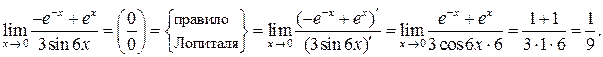
Следовательно, 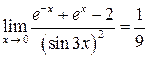 .
.
Ответы: а) 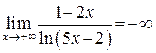 ; б)
; б) 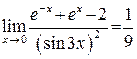 .
.
Решение задачи 4а
Проведем полное исследование функции 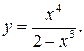
1) ООФ: 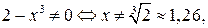 т. е.
т. е. 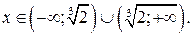
2) Функция не может быть четной или нечетной, так как имеет
несимметричную относительно начала координат ООФ. Следовательно, эта функция общего вида, симметрию графика предсказать нельзя. Функция непериодическая.
3) Функция непрерывна на всей ООФ, так как является элементарной функцией. Точка 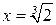 является точкой разрыва, так как функция не определена в этой точке, но определена в ее окрестности.
является точкой разрыва, так как функция не определена в этой точке, но определена в ее окрестности.
Для определения типа разрыва найдем односторонние пределы при
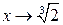 :
: 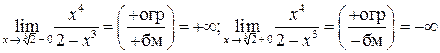
(здесь при 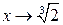 числитель является ограниченной функцией, а знамена-тель – бесконечно малой). Следовательно, в точке
числитель является ограниченной функцией, а знамена-тель – бесконечно малой). Следовательно, в точке 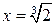 функция терпит бесконечный разрыв и
функция терпит бесконечный разрыв и 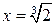 – уравнение вертикальной асимптоты.
– уравнение вертикальной асимптоты.
4) Промежутки монотонности и экстремумы найдем при помощи 1-й производной:
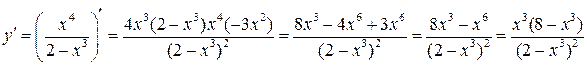 .
.
Критические точки по 1-й производной: 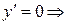 х = 0, х = 2;
х = 0, х = 2; 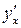
не существует 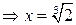 .
.
Точка 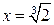 не является критической точкой, так как
не является критической точкой, так как 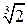 Ï ООФ.
Ï ООФ.
Следовательно, имеем две критические точки: х = 0 и х = 2.
Проверим выполнение достаточных условий монотонности и экстре-мума по знаку 1-й производной. На рис. 30 видно, что функция возрастает на интервалах 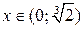 и
и 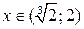 , убывает на интервалах
, убывает на интервалах 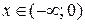
и 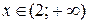 .
.
 В точке х = 0 есть минимум функции,
В точке х = 0 есть минимум функции, 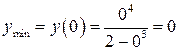 , в точке х = 2 есть максимум,
, в точке х = 2 есть максимум, 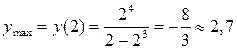 .
.
5) Выпуклость, вогнутость графика и точки перегиба исследуем при помощи 2-й производной:
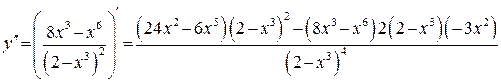
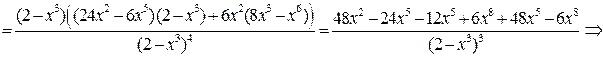
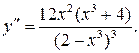
Критические точки по 2-й производной: 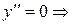 х = 0,
х = 0, 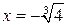 ;
; 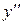 не существует Þ x =
не существует Þ x = 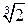 . Точка
. Точка 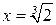 не является критической точкой, так как
не является критической точкой, так как 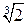 Ï ООФ. Следовательно, критическими точками по второй
Ï ООФ. Следовательно, критическими точками по второй
производной являются точки х = 0 и 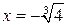 .
.
 Проверим выполнение достаточных условий выпуклости, вогнутости графика функции по знаку 2-й производной. На рис. 31 видно, что график функции выпуклый на интервалах
Проверим выполнение достаточных условий выпуклости, вогнутости графика функции по знаку 2-й производной. На рис. 31 видно, что график функции выпуклый на интервалах 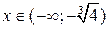 ,
, 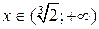 и вогнутый на интервале
и вогнутый на интервале 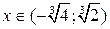 . В точке
. В точке
с абсциссой 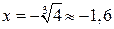 имеется пере-гиб графика,
имеется пере-гиб графика, 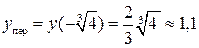 .
.
6) Найдем наклонные асимптоты графика y = kx + b при 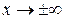
по формулам (26), (27):
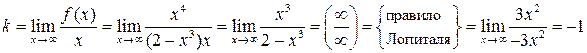 ;
;
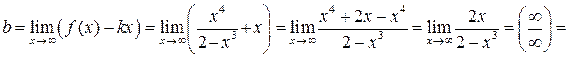
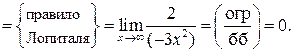
Следовательно, наклонная асимптота графика имеет уравнение 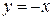 .
.
7) Точка пересечения с осями координат – единственная: (0; 0), так как
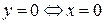 .
.
8)  Построение графика начинаем с построения асимптот
Построение графика начинаем с построения асимптот 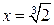 и
и 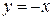 , затем отмечаем точки графика, в которых функция имеет экстремумы: точку минимума (0; 0), точку максимума
, затем отмечаем точки графика, в которых функция имеет экстремумы: точку минимума (0; 0), точку максимума 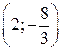 , и точку перегиба
, и точку перегиба 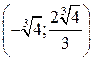 . После этого выполняем построение гра-фика функции
. После этого выполняем построение гра-фика функции 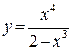 сначала на промежутках
сначала на промежутках 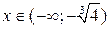 и
и 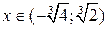 , затем на промежутке
, затем на промежутке 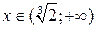 .
.
На графике (рис. 32) видны сближение кривой с асимптотами при уда-лении от начала координат и перегиб кривой.
Ответ: график на рис. 32.
Решение задачи 4б
Проведем полное исследование функции 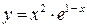 .
.
1) ООФ: 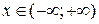 , ОЗФ:
, ОЗФ: 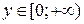 , так как
, так как 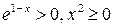 .
.
2) Функция не является четной или нечетной, так как 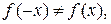
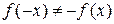 . Следовательно, эта функция общего вида. Функция непериодическая.
. Следовательно, эта функция общего вида. Функция непериодическая.
3) Функция непрерывна на всей ООФ. Точек разрыва нет.
4) Промежутки монотонности и экстремумы найдем при помощи 1-й производной:
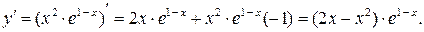
Критические точки по 1-й производной: 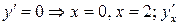
не существует – таких точек нет.
 Проверим выполнение достаточных условий монотонности и экстре-мума по знаку 1-й производной. На рис. 33 видно, что функция возрастает на интервале
Проверим выполнение достаточных условий монотонности и экстре-мума по знаку 1-й производной. На рис. 33 видно, что функция возрастает на интервале 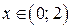 , убывает на интервалах
, убывает на интервалах 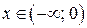 и
и 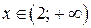 .
.
|
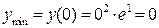 , в точке х = 2 максимум,
, в точке х = 2 максимум, 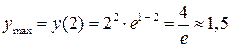 .
.
5) Выпуклость, вогнутость графика и точки перегиба исследуем при помощи 2-й производной:
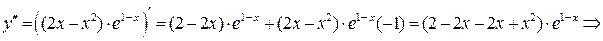
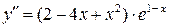 .
.
Критические точки по 2-й производной: 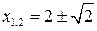 , т. е.
, т. е. 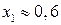 ,
, 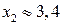 .
.
Проверим выполнение достаточных условий выпуклости, вогнутости графика функции по знаку 2-й производной. На рис. 34 видно, что график функции выпуклый на интервале 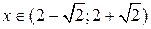 , и вогнутый на интервалах
, и вогнутый на интервалах 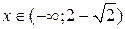 и
и 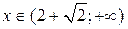 .
.
|
 В точках с абсциссами
В точках с абсциссами 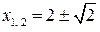 имеются перегибы графика; вычисляем ординаты точек перегиба:
имеются перегибы графика; вычисляем ординаты точек перегиба: 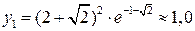 ,
, 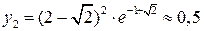 .
.
6) Найдем наклонные асимптоты графика y = kx + b при 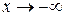 и при
и при 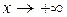 (отдельно) по формулам (26), (27).
(отдельно) по формулам (26), (27).
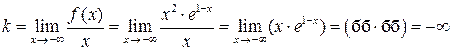
(здесь при 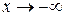 обе функции под знаком предела являются бесконечно большими). Следовательно, при
обе функции под знаком предела являются бесконечно большими). Следовательно, при 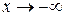 наклонных асимптот нет.
наклонных асимптот нет.
При 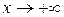 получаем:
получаем:
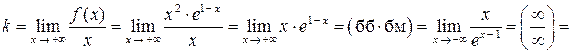
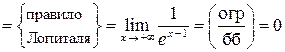 ;
;
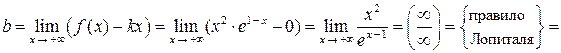
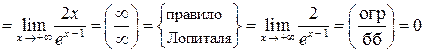 . Следовательно, при
. Следовательно, при 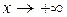 график имеет горизонтальную асимптоту, ее уравнение: у = 0.
график имеет горизонтальную асимптоту, ее уравнение: у = 0.
7) Точка пересечения с осями координат – единственная: (0; 0), так как
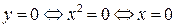 .
.
8)  Построение графика начинаем с построения асимптоты у = 0 (она совпадает с осью абсцисс), затем отмечаем точки графика, в которых функция имеет экстремумы: точку минимума (0; 0), максимума
Построение графика начинаем с построения асимптоты у = 0 (она совпадает с осью абсцисс), затем отмечаем точки графика, в которых функция имеет экстремумы: точку минимума (0; 0), максимума 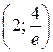 , и точки
, и точки
перегиба (x1; y1) и (x2; y2), где 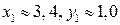 ,
,  . После этого выполняем построение графика функции
. После этого выполняем построение графика функции 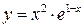 сначала на промежутках
сначала на промежутках 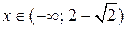 и
и 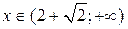 , затем на промежутке
, затем на промежутке 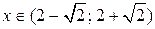 .
.
На графике (рис. 35) видно сближение кривой с асимптотой у = 0 при 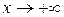
и перегибы кривой.
Ответ: график на рис. 35.
Рекомендуемая литература
1. Письменный, Д.Т. Конспект лекций по высшей математике. В 2 ч. Ч. 1 / Д.Т. Письменный. – М. : Айрис-пресс, 2003. – 288 с.
2. Шипачев, В.С. Высшая математика : учебник для вузов / В.С. Шипачев. – М. : Высш. шк., 1998. – 479 с.
3. Данко, П.Е. Высшая математика в упражнениях и задачах. В 2 ч. Ч. 1 / П. Е. Данко, А.Г. Попов, Т.Я. Кожевникова. – М. : Высш. шк., 1999. – 304 с.
4. Шипачев, В.С. Задачник по высшей математике / В.С. Шипачев. – М. : Высш. шк., 2001. – 304 с.
|
Дата добавления: 2019-05-21; просмотров: 1171;











