Непрерывность функции, точки разрыва
Функция 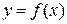 называется непрерывной в точке х0, если:
называется непрерывной в точке х0, если:
1) x0 Î ООФ вместе с некоторой своей окрестностью;
2) существует конечный предел 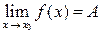 ;
;
3) этот предел совпадает со значением функции в точке х0, т. е.
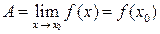 . (9)
. (9)
Все элементарные функции непрерывны в каждой точке своей области определения.
Если функция не является непрерывной в точке х0, но она определена в окрестности этой точки (за исключением, быть может, самой точки х0), то х0 называется точкой разрыва функции.
Для определения вида разрыва в точке х0 находят односторонние
пределы 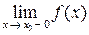 и
и 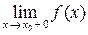 . При этом:
. При этом:
если существуют односторонние пределы 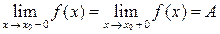 , но
, но 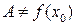 , то говорят, что функция терпит в точке х0 разрыв типа выколотой точки;
, то говорят, что функция терпит в точке х0 разрыв типа выколотой точки;
если существуют односторонние пределы 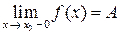
и 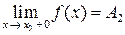 , но
, но 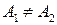 , то
, то 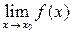 не существует; в этом случае
не существует; в этом случае
говорят, что функция терпит в точке х0 разрыв типа"скачок";
если левосторонний либо правосторонний (или оба) пределы функции при 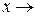 х0 бесконечные, то говорят, что функция терпит в точке х0 бесконечный разрыв.
х0 бесконечные, то говорят, что функция терпит в точке х0 бесконечный разрыв.
Разрывы типа выколотой точки и типа "скачок" относятся к конечным разрывам, или разрывам I рода, бесконечные разрывы относятся к разрывам II рода.
Примеры.
1) Функция 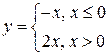 непрерывна
непрерывна 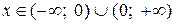 в силу непрерывности функций y = –х и y = 2х. В точке х = 0 функция также
в силу непрерывности функций y = –х и y = 2х. В точке х = 0 функция также
непрерывна, так как
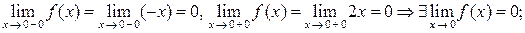
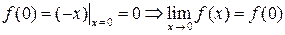 .
.
Следовательно, функция непрерывна для всех 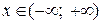 (рис. 9).
(рис. 9).
2) Функция 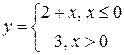 непрерывна
непрерывна 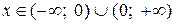 в силу непрерывности функций y = 2 + х и y = 3. В точке х = 0 функция терпит разрыв типа"скачок" (рис. 10), так как
в силу непрерывности функций y = 2 + х и y = 3. В точке х = 0 функция терпит разрыв типа"скачок" (рис. 10), так как 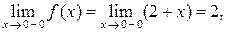
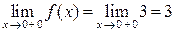 , следовательно,
, следовательно, 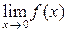 не существует.
не существует.
3) Функция y = tg x непрерывна во всех точках своей ООФ, т. е. для 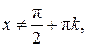
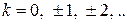 . В точках
. В точках 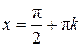 функция терпит разрывы
функция терпит разрывы
II рода (рис. 11), так как 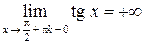 ;
; 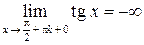
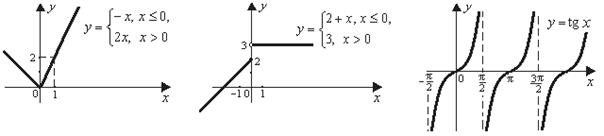
Рис. 9 Рис. 10 Рис. 11
Комплексные числа
Комплексным числом называется выражение вида
z = x + iy, (10)
где х, у – действительные числа, а i – мнимая единица, т. е. число, для
которого выполнено равенство i2 = –1.
Если х = 0, то комплексное число z = 0 + iy называется чисто мнимым.
Если у = 0, то комплексное число z = x + i0 = х является действительным, в частности, если х = у = 0, то z = 0.
На множестве комплексных чисел алгебраическое уравнение n-й
степени вида 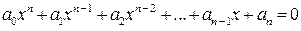 , где ak – числа,
, где ak – числа, 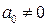 ,имеет ровно n корней.
,имеет ровно n корней.
Пример. Решим уравнение: х2 + 9 = 0.
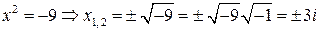 .
.
Следовательно, уравнение имеет 2 корня: 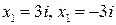 .
.
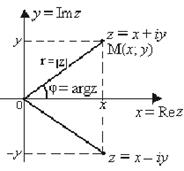 На координатной плоскости Оху комплексное число z = x + iy можно изобразить точкой М(х; у) или радиус-вектором этой точки
На координатной плоскости Оху комплексное число z = x + iy можно изобразить точкой М(х; у) или радиус-вектором этой точки 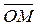 (рис. 12), где х = Re z – действительная часть числа z, у = Im z – мнимая часть числа.
(рис. 12), где х = Re z – действительная часть числа z, у = Im z – мнимая часть числа.
|
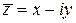 называется сопряженным комплексному числу
называется сопряженным комплексному числу 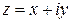 . Геометрически точки z и
. Геометрически точки z и 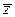 симметричны относительно оси Ох (рис. 12).
симметричны относительно оси Ох (рис. 12).
Модулем комплексного числа называется действительное неотрицательное число 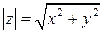 . Геометрически модуль комплексного числа
. Геометрически модуль комплексного числа 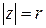 – это модуль вектора
– это модуль вектора 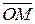 (рис. 12).
(рис. 12).
Комплексное число можно задать либо парой действительных чисел (декартовы координаты точки (х; у)), либо его модулем и величиной угла φ между вектором 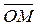 и положительным направлением оси Ох (полярные координаты точки (r; φ)). Величина угла φ называется аргументом комп-лексного числа.
и положительным направлением оси Ох (полярные координаты точки (r; φ)). Величина угла φ называется аргументом комп-лексного числа.
Аргумент комплексного числа определен неоднозначно, а с точностью до слагаемого 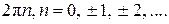 . Значение аргумента, заключенное
. Значение аргумента, заключенное
в промежутке 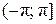 , называется главным значением аргумента и обозначается arg z, тогда можно записать:
, называется главным значением аргумента и обозначается arg z, тогда можно записать:
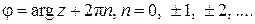 (11)
(11)
Для комплексного числа z = 0 аргумент не определен, его модуль r = 0.
Запись комплексного числа в виде (10) называют алгебраической
формой комплексного числа.
Если использовать формулы связи между декартовыми и полярными координатами 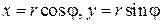 , то можно записать тригонометрическую форму комплексного числа:
, то можно записать тригонометрическую форму комплексного числа:
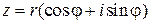 , (12)
, (12)
где
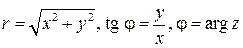 . (13)
. (13)
Для определения главного значения аргумента можно использовать формулы:
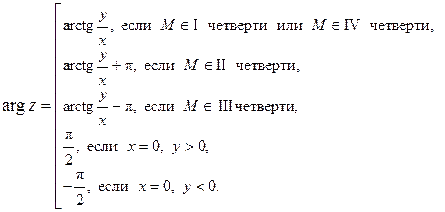 (14)
(14)
Пример. Получим тригонометрическую форму комплексного числа z = –2 – 2i, используя формулы (13) и (14).
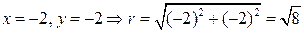 ,
,
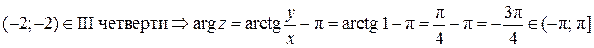 ,
,
следовательно, тригонометрическая форма комплексного числа z для 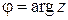 имеет вид:
имеет вид:
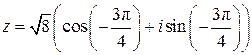 .
.
Дата добавления: 2019-05-21; просмотров: 677;











