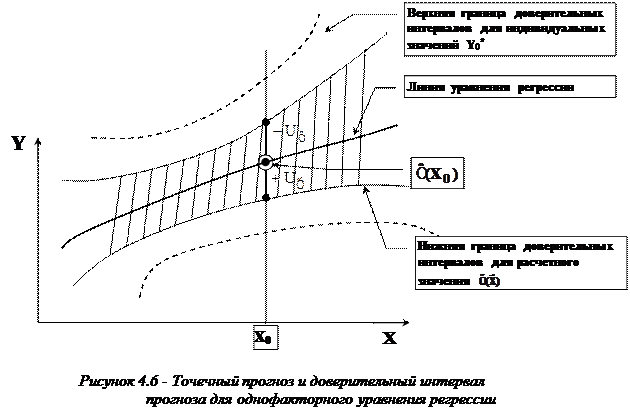
Точечный прогноз и оценка доверительных интервалов прогноза

Найдем средние квадратические отклонения, которые потребуются нам при получении полуширины доверительных интервалов прогноза для:

· коэффициентов регрессии ;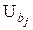

· расчетного значения моделируемой величины 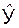или, что тоже самое условного математического ожидания M_x(Y) ;

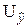· индивидуальных значений случайной величины Y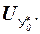

1) Среднее квадратичное отклонение фактических наблюдений 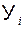относительно срединной поверхности регрессии 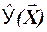( в одном случае – относительно линии регрессии :

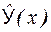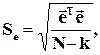(4.35)

где k – число членов в уравнении регрессии; 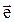– вектор случайных остатков.

2) Среднее квадратическое отклонение для случайных величин – коэффициентов регрессии:

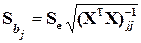(4.36)

Здесь 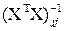– диагональный элемент с номером строки j в информационной матрице Фишера.

3) Среднее квадратическое отклонение расчетного значения :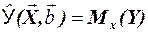

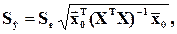(4.37)

где 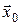– значение вектора регрессоров в точке прогноза; «Т» – знак транспортирования.

4) Среднее квадратическое отклонение для индивидуальных значений 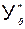случайной величины Y в точке прогноза :

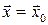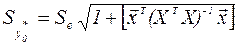(4.38)

5) Полуширина доверительного интервала :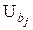

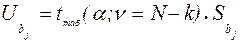(4.39)

6) Полуширина доверительного интервала :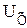

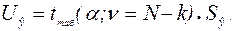(4.40)

7) Полуширина доверительного интервала для разброса индивидуальных значений Y:

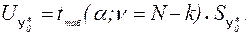(3.41)