Матричная форма метода наименьших квадратов.

4.3.1.Уравнение наблюдений в матричной форме

Запишем наблюдения в каждой точке i:

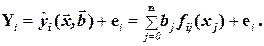(4.4)

Введем в рассмотрение матрицу плана наблюдений или матрицу базисных функций (не путать с вектором ).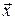

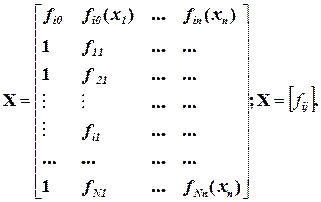(4.5)

Тогда при условии линейного вхождения вектора параметров 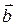в модель, получим:

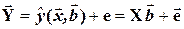(4.6)

Справедливость уравнения (4.6) проверяется переводом уравнения (4.6) в скалярную форму по правилу умножения матрицы X на вектор .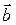

В уравнении наблюдений (4.6)

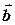= (b₀,b₁,….,b_j,….b_n); - n –мерный вектор оцениваемых параметров;

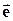= (e₀,e₁,….,e_j,….e_n); - N –мерный вектор остатков;

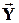= (y₀,y₁,….,y_j,….y_n); - N –мерный вектор наблюдений.

Замечание: Если структура модели нелинейна по 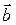, т.е. 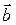входит в базисную функцию, то записать уравнение (4.6) невозможно и классический метод наименьших квадратов непримерим.

4.3.2.Нормальные уравнения регрессии и формула для параметров уравнения

Используем известную формулу из матричной алгебры:

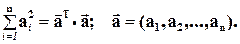(4.7)

Тогда, опуская стрелки с учетом того, что 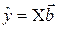получаем:

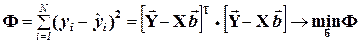(4.8)

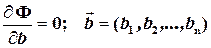(4.9)

Система нормальных уравнений запишется в виде:

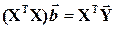(4.10)

где (X^TX) – матрица нормальных уравнений.

Пусть обратная матрица (X^TX)^-1 существует (она называется информационной матрицей Фишера). Тогда:

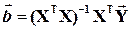
В противном случае det(X^TX)^-1=0 и матрица нормальных уравнений необратима.

Если det(X^TX)^-1¹0, но очень мал, то обращаемая матрица плохо обусловлена. Возникает вычислительные проблемы обращения матриц большей размерности.