Оценка адекватности уравнения регрессии (проверка гипотез о предпосылках метода наименьших квадратов)

4.6.1.Гипотеза о близости к нулю математического ожидания остатков

Здесь используется критерий Стьюдента для остатков и проверяется нуль-гипотеза:

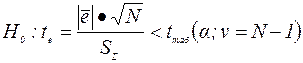(4.17)

S_å - среднее квадратичное отклонение остатков – мера рассеяния остатков относительно своего среднего

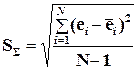(4.18)

Замечание: Здесь число степеней свободы S_å=(N – 1), так как на вычисление среднего (центра рассеяния) расходуется одна степень свободы:

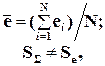(4.19)

где S_e- среднее квадратичное отклонение наблюдений Y_i относительно поверхности регрессии :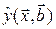

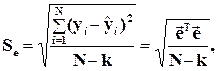(4.20)

где, k – число членов уравнения регрессии, включая свободный член.

3.6.2. Гипотеза о статистической значимости коэффициентов регрессии b_j

Используя t – критерий Стьюдента проверяем нуль гипотезу:

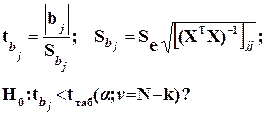(4.21)

Выводы:

· Если данное неравенство выполнено, то коэффициент b_j – статистически не значим.

· Если все коэффициенты в уравнение регрессии не значимы то уравнение регрессии не значимо: влияние регрессоров Х_j на формирование значений Y не различимо на фоне случайных возмущений {E}. Модель не адекватна.

· Если все коэффициенты уравнения регрессии значимы, то нарушение адекватности в данном пункте (по данной гипотезе) нет. Но вывод об адекватности делать рано, должны быть выполнены все предпосылки метода наименьших квадратов.

· Если часть коэффициентов уравнения регрессии значима, а часть не значима, то это не является снованием для нарушения адекватности. Значимая часть регрессоров может адекватно описывать объект.

· Незначимые коэффициенты уравнения регрессии и соответствующие им регрессоры следует исключить из модели: они не несут никакой полезной информации.

4.6.3. Гипотеза о статистической значимости всего уравнения регрессии в целом

Используется критерий Фишера-Снедекора F и проверяется нуль-гипотеза:

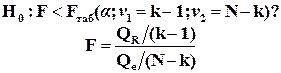(4.22)

Q_R – сумма квадратов отклонений расчетных значений 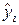от среднего 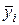, обусловленная вариацией факторов; Q_e - сумма квадратов отклонений расчетных значений 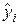от фактически наблюдаемых, обусловленная влиянием случайных возмущений E_i (включая влияние неучтенных в модели факторов).

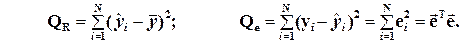
Выводы:

1. Если гипотеза Н₀ выполнена, то уравнение регрессии в целом статистически незначимо и можно сразу делать вывод о неадекватности модели.

2. Если нуль-гипотеза Н₀ не выполнена, т.е. F>F_таб, то уравнение регрессии в целом значимо и можно переходить к проверке других гипотез.

4.6.4. Оценка качества уравнения регрессии

Для комплексной оценки качества уравнения регрессии используется коэффициент детерминации R²

Коэффициент детерминации R² как мера качества уравнения регрессии характеризует долю вариации зависимой переменной, обусловленную регрессией (влиянием факторов), в общей вариацией результативной переменной Y_i ; чем ближе коэффициент детерминации R² к единице, тем лучше уравнение регрессии аппроксимирует экспериментальные данные, тем ближе эмпирические точки располагаются к линии регрессии, тем больше прогностическая сила модели.

Замечание: Коэффициент множественной детерминации, определяется по результатам линейного корреляционного анализа, не следует смешивать с рассматриваемым коэффициентом детерминации R², справедливого и для моделей, нелинейных по регрессорам (в этом случае его следует называть «индексом множественной детерминации»). Другими словами,

R²¹[R_j.₁₂…_m]².

Это разные коэффициенты: первый из них связан с регрессионным анализом, т.е. привязан к конкретной параметрической модели 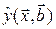, а второй связан корреляционным анализом линейно-связанных случайных величин, т.е. с корреляционной матрицей K. Сходство только в термине «детерминация», а расчетные формулы – разные:

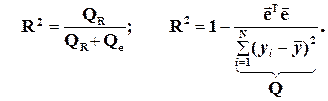(4.23)

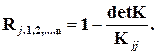(4.24)

Последняя формула справедлива только для линейных корреляционных связей.

Приемы улучшения качества модели:

1). Сделать предварительное сглаживание временного ряда одномерного или многомерного по методу простой скользящей средней или экспоненциального сглаживания. Данный прием применяют только при наличии упорядочного наблюдения во времени, т.е. для использования данных пространственного типа он не применяется.

2). Использовать нормирование всех переменных и зависимых и независимых:

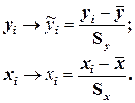(4.25)

Выводы:

1. Приемлемость получаемого значения R² определяется целями моделирования: если допустимы грубые (прикидочные) оценки, то можно принять R² ~ 0,8, для более точных оценок R² > 0,9.

2. Если база данных (БД) сильно зашумлена (или даже сознательно искажена, что имеет место в задачах налогового и финансового контроля), то может оказаться, что никакие ухищрения не позволяют получить R²>0,9.

Рекомендации:

Повысить информативность базы данных за счет различных алгоритмов предпроцессорной обработки (сглаживание, если база данных упорядочена по времени; кластеризации данных; компрессия данных (факторный анализ); расширения бахзы данных как парирование ее зашумленности; накнец – переход к другим моделям:

- нейросетевым

- нечетким;

- фрактальным.

4.6.5. Скорректированный коэффициент детерминации

Недостаток нескорректированного коэффициента детерминации в том, что R² увеличивается при введении новых факторов, хотя качество уравнения регрессии может и не возрастать, т.е. вводимые регрессоры оказываются малозначимыми. Скорректированный (адаптивный) коэффициент множественной детерминации определяется по формуле:

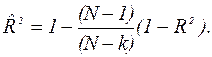(4.26)

В отличие от не скорректированного коэффициента детерминации R² этот коэффициент может в принципе уменьшается при увеличении числа регрессоров (за счет знаменателя второго члена), если эти дополнительные регрессоры малозначимы, т.е. 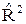более информативен, чем R², но с одной оговоркой: для вновь вводимых регрессоров критерий Стьюдента должен быть больше 1 по модулю:

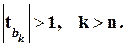
4.6.6. Проверка гипотезы о чисто случайном характере остатков

Здесь может быть два случая:

Случай а): База данных упорядочена по времени: вектор – строки (или кортежи 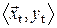) расположены в порядке возрастания времени, т.е. образует многомерный временной ряд.

t_i=t₁,t₂,…..t_n; t_n>t_i-1 , "_i=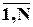

В этом случае можно применить для оценки чисто случайного характера остатков {е} два критерия:

- поворотных точек, либо критерий Фостера- Стьюарта (отсутствие тренда в остатках).

- Критерий Дарбина – Уотсона (отсутствие автокорреляции в остатках)

1) При проверке гипотезы об отсутствии временного тренда в остатках по критерию поворотных точек проверяется нуль гипотеза:

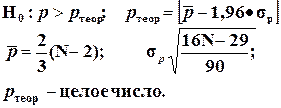(4.27)

Если неравенство истинно, т.е. экспериментальное число поворотных точек p, определяемое по графику, меньше теоретического, то означает что имеется тренд в остатках и остатки не являются чисто случайными.

Если неравенство нарушено, то тренда в остатках нет, и их можно считать случайными, как не содержащие тренда.

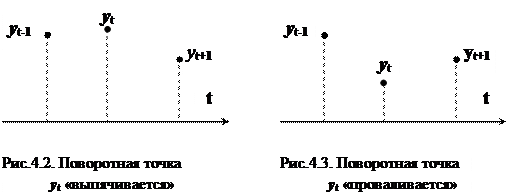
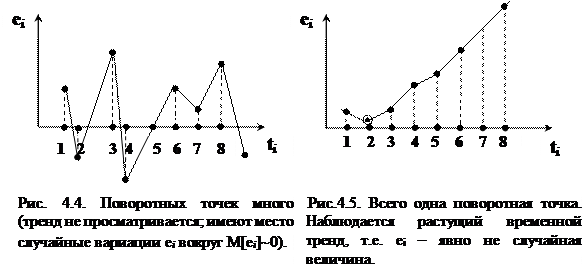
Если нуль-гипотеза Н₀ выполняется, то временного тренда нет.

2. Проверка гипотезы о наличии автокорреляции в остатках по критерию Дарбина-Уотсона

Автокорреляция – это корреляция между членами одного временного ряда.

Здесь можно испльзовать d – статистику Дарбина-Уотсона:

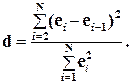(4.28)

Смысл этого критерия: чем меньше разность суммируемых членов, тем сильнее проявления «последействия», т.е. влияния предыдущего остатка на последующий и тем вероятнее наличие автокорреляции остатков.

Замечание:

1. Если d>2, то перед входом в таблицу теоретических значений d-критерия надо сделать преобразование переменных:

d®d^¢ = 4-d

Выводы:

_· Автокорреляция имеет место, остатки не являются чисто случайными, нарушена адекватность модели, если d < d_таб.min.

· Ничего сказать об автокорреляции енльзя, нужно использовать другие критерии, если d Î [d_таб.min; d_таб.max].

· Автокорреляция отсутствует, нарушений адекватности нет, если

d > d_таб.max.

При не определенной ситуации применяются другие критерии. В частности, можно использовать первый коэффициент автокорреляции, т.е. коэффициент линейной парной корреляции между соседними членами временного ряда е_t, е_t-1:

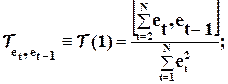(4.29)

(4.30)

Случай б): База данных не упорядочена во времени (например, при социологических опросах, данные по разным странам т.д.)

В этих случаях упомянутые выше критерии поворотных точек, Фостера- Стьюарта, Дарбина- Уотсона в принципе неприменимы. Вместо них проверяется тест на отсутствие гетероскедастичности, т.е. корреляции между регрессорами 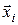и остатками .

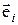Тест Уайта: строится линейное уравнение регрессии для квадратов остатков:

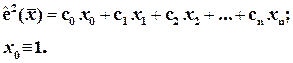(4.31)

Гипотеза о статистической значимости линейного уравнения регрессии для квадратов остатков в целом проверяется по критерию Фишера-Стьюдента, точно так же как и для основного уравнения регрессии.

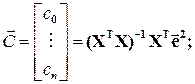(4.32)

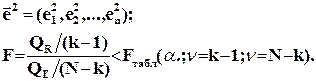(4.33)

Вывод:

Если нуль-гипотеза для критерия Фишера выполняется, то гетероскедастичности нет

Если неравенство не выполняется, то это означает что гетероскедастичность есть.

4.6.7. Проверка гипотезы о нормальном законе распределения остатков

Используется (R/S) - критерий, т.е. нормированный размах остатков:

(R/S) = (е_max-е_min)/S_e,(4.34)

где S_e определяется формулой (3.20).

Вывод:

Если 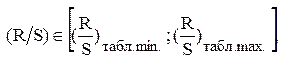, то гипотеза о нормальном законе распределение остатков {е_i} не отвергается.

В противном случае – отвергается.

Общий вывод:Если все 6 гипотез, рассмотренные выше, о предпосылках метода наименьших квадратов выполняются и критерии качества модели R² приемлемы для поставленных целей моделирования, то модель считается адекватной и пригодна для практического применения.

Замечание.Если выборка деформируется (сужается или расширяется) либо изменяется принимаемый уровень значимости a оценок, то проверку адекватности надо делать заново.