Коэффициент ранговой корреляции
Коэффициент ранговой корреляции служит числовой мерой стохастической связи между качественными (нечисловыми) показателями
Качественные показатели называют также ординальными и порядковыми переменными.
Пример:
На соревнованиях по фигурному катанию получена таблица оценок за «технику» Ti и «артистичность» Si (два качественных признака).
| Номер оценки | Ранги | |
| оценка за «технику» | оценка за «артистичность» | |
| признак X | признак Y | |
| i | Ti | Si |
| T1 | S1 | |
| T2 | S2 | |
| …. | …. | …. |
| N | TN | SN |
Здесь Ti, Si –ранги (баллы), т.е. значения ординальных переменных, которые находятся путем экспертных оценок (оценки судей).
Выборочная оценка, коэффициента ранговой корреляции Спирмена определяется по формуле
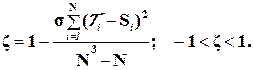 (3.23)
(3.23)
N – число наблюдений (строк).
Значимость коэффициента ранговой корреляции Спирмена проверяется аналогично (3.9) по критерию Стьюдента.
Тема 4. МНОЖЕСТВЕННЫЙ РЕГРЕССИОННЫЙ АНАЛИЗ
Постановка задачи
Будем постулировать выполнение основной предпосылки эконометрического анализа (2.1) – (2.5).
Пусть имеется выборка пространственного типа, т.е. кортежи наблюдений:
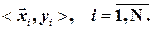
1). Требуется получить уравнение регрессии, для объясненной части Mx(Y) случайной величины Y, т.е. получить параметрическую оценку:
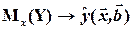
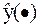 – общем случае нелинейная функция.
– общем случае нелинейная функция.
2). Требуется также, провести статистический анализ остатков {еi}, т.е. установить: адекватна ли модель. И оценить ее погрешность.
Замечание 1: Всю теорию регрессионного анализа мы будем излагать для аддитивной формы (структуры) модели которая более наглядно интерпретируется: виден отдельный вклад каждого выходного фактора:
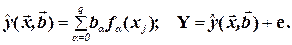 (4.1)
(4.1)
В частном случае, когда в структуре модели на каждый входной фактор выделена одна базисная функция имеем:
fa(xj)ºfj(xj); aºj; q=n; f0º1.
Пример:
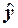 =b0f0(x0) + b1x1 + b2lnx2; f0(x0)º1; f1=x11; f2ºlnx2.
=b0f0(x0) + b1x1 + b2lnx2; f0(x0)º1; f1=x11; f2ºlnx2.
Здесь каждый член отражает вклад своего фактора, в общем случае нелинейный.
Замечание 2: Вид координатных функций fa(xj) выбирается в соответствии с особенностями моделируемого объекта. Это могут быть функции:
- степенные;
- показательные;
- экспотенциальные;
- логарифмические;
- тригонометрические и др.
Для колебательных процессов, например сезонных колебаний, хорошо подходят гармонические функции. Удобно подбирать вид базисных функций fa(xj)с помощью инструмента МS Excel «Мастер диаграмм».
Дата добавления: 2020-12-11; просмотров: 472;











