Метод наименьших квадратов (МНК) в скалярной форме

Используя уравнение регрессии (4.1), запишем функцию цели Ф, характеризующую качество аппроксимации объясненной части Y_e=M_x(Y) уравнением регрессии:

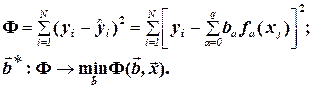(4.2)

Это задача безусловной оптимизации, т.е требуется найти такие оптимальные значения 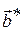вектора параметров уравнения регрессии, которые доставляют минимум функции цели Ф.

Замечание: Для простоты далее считаем, что в уравнении регрессии каждый входной фактор x_j предоставлен одним членом суммы со своей базисной функцией f_j(x_j), т.е. aºj.

В теории регрессионного анализа показано, что функция Ф непрерывна и строго выпукла по аргументам b_j. Тогда ее минимум обеспечивается условиям

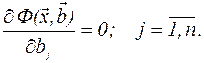(4.3)

Система (4.3) называется системой, нормальных уравнений. Если вектор 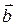входит в модель линейно, то эта система представляет собой линейные алгебраические уравнения относительно искомых {bj}, j= .

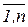Замечание: Под линейным вхождением {bj}, в модель понимается, что сами координаторные функции {f_j(x_j)} могут быть нелинейными, но они не должны содержать ни одного оцениваемого параметра bj.

Пример:

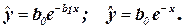
Здесь обе модели нелинейны по независимой переменной х. Однако вторая модель линейна по искомому параметру b₀ , в тоже время как в первой модели параметр b₁ входит в структуру модели нелинейно.

Если система нормальных уравнений, есть система линейных алгебраических уравнений, то для ее решения можно использовать аппарат линейной алгебры и, соответственно, матричную форму метода наименьших квадратов.