Числовые меры корреляционной связи

3.2.1. Ковариация

Приставка «Ко» означает «совместный» (ковариация – взаимосвязанная или совместная вариация). Генеральное значение ковариации определяется формулой:

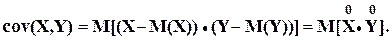(3.1)

Здесь М[·] - оператор вычисления математического ожидания, нуль вверху означает центрирование величины.

Заметим что в формуле (3.1) вариация случайных величин Y и X измеряется их отклонением от математических ожиданий, а условие «совместности» измерения вариаций реализуется операцией умножения внутри квадратных скобок.

3.2.2. Выборочная оценка коэффициента линейной парной корреляции

На практике вместо генеральной совокупности мы имеем выборку из неё. Будем считать выборку репрезентативной, а связь между случайными величинами Y и X – линейной:

y = b₀ + b₁x,(3.2)

где b₀, b₁ – генеральные (теоретические) значения параметров линейного уравнения регрессии (3.2.), которые будем обозначать греческими буквами, а их выборочные оценки b₀, b₁ – латинскими малыми буквами.

Если нормировать ковариацию (3.1), т.е. разделить ее на произведение средних квадратических отклонений (СКО) 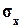и 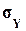, то получим коэффициент парной корреляции. Генеральное значение коэффициента равно:

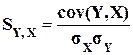(3.3.)

а выборочная оценка:

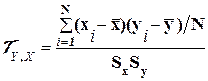(3.4.)

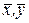- выборочные оценки математических ожиданий m_x, m_y;

S_x,S_y – выборочные СКО.

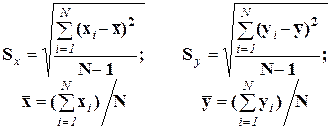(3.5)

Знак при T определяет форму (характер) корреляционной связи в уравнении (3.2):

(+) положительный знак соответствует возрастающему виду (при росте случайной величины х другая случайная величина тоже работает в среднем);

( - ) отрицательный знак соответствует убывающему виду, зависимости (3.2).

Таким образом коэффициент линейной парной корреляции изменяется в пределах .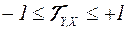

3.2.3. Математический смысл коэффициента линейной парной корреляции

Предположим, что между двумя случайными величинами X и Y в среднем существует линейная связь (3.2), т.е. они связаны линейным уравнением регрессии для математических ожиданий

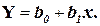(3.6)

При взгляде на уравнение регрессии видно, что измерителем связи Y и X может служить коэффициент b₁. Действительно, вычисляя производную от функции 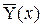, получим:

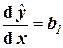
т.е. b₁ оценивает скорость изменения функции Y при изменении аргумента X. Однако b₁ неудобен как измеритель связи тем, что b₁ зависит от единиц измерения X и Y. Хотелось бы иметь безразмерный показатель. Сделаем это, переходя к нормированным переменным в уравнении регрессии:

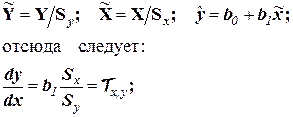(3.7)

Коэффициент корреляции T_x,y есть скорость изменения (производная) нормированной функции 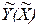при вариации нормированного аргумента 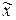и линейной связи между ними.

3.2.4. Статистический смысл коэффициента линейной парной корреляции

Запишем производную в приращениях:

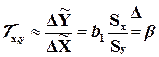(3.8)

Заметим, что здесь b – это так называемый в регрессионном анализе бэтта-коэффициент.

Коэффициент линейной парной корреляции показывает на сколько процентов (%)(в долях от СКО S_y) изменяется случайная величина Y, если другая величина X измениться на 1% в долях от своего СКО S_x.

3.2.5. Геометрическая интерпретация коэффициента корреляции

Геометрическую интерпретацию коэффициента линейной парной корреляции как измерителя силы связи между случайными величинами Y и X можно уяснить из рисунку 3.1.

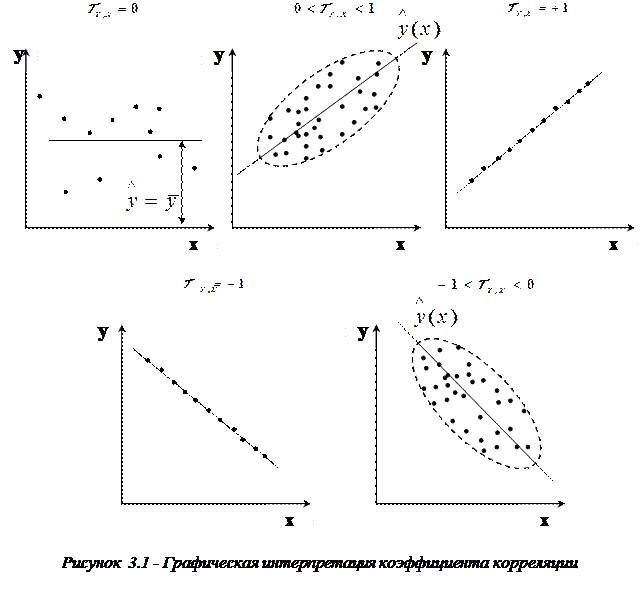
где:

а) – связь между Y и X в среднем отсутствует (коэффициент b₁ в (3.6) равен нулю);

б) – возрастающая (в среднем) статистическая зависимость Y от X (b₁>0);

в) – возрастающая детерминированная (функциональная) связь Y и X;

г) – падающая детерминированная (функциональная) зависимость;

д) – падающая статистическая зависимость.