Множественный корреляционный анализ

Как правило экономический процесс описывается числом показателей, более двух, т.е. вектором случайных величин:

X=(X₁, X₂….., X_j…., X_m)

j - номер показателя (фактора)

3.4.1. Корреляционная матрица

Пусть совокупность {Xj} имеет совместный нормальный закон распределения. Тогда, как и ранее, взаимосвязь между двумя показателями Xi и Xj можно описать коэффициентом парной линейной корреляции Tij. Множество всех возможных сочетаний{Tij }, i,j= 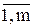образует квадратную корреляционную матрицу:

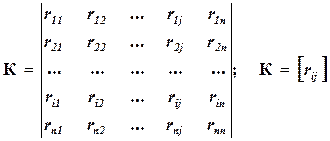(3.11)

Отметим важные свойства корреляционной матрицы

1). Все диагональные элементы этой матрицы равны единице:

daig K = Tji = 1

2). Корреляционная матрица – симметричная, т.е. ее элементы, симметричные относительно главной диагонали, равны друг другу:

Tij = Tji,

так как произведение в формуле (3.4) для Tij не зависит от порядка следования сомножителей.

3.4.2. Выборочный коэффициент множественной корреляции

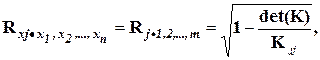Коэффициент множественной корреляции определяет тесноту связи одного показателя с совокупностью остальных (n-1) показателей при их одновременном действии:

(3.12)

Kjj – алгебраическое дополнение элемента Tjj матрицы К.

Коэффициент множественной корреляции изменяется от 0 до +1, т.е. всегда неотрицателен.

3.4.3. Частный коэффициент корреляции

Частный коэффициент корреляции служит количественной мерой связи случайных величин Xi и Xj при условии исключения влияния других случайных (m-2) величин, т.е. при их фиксации.

Выборочная оценка коэффициента частной корреляции определяется по формуле:

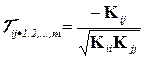(3.13)

где Kij, Kjj – алгебраическое дополнение соответствующих элементов матрицы К.

Частный коэффициент корреляции так же, как и парный коэффициент линейной парной корреляции, изменяется от -1 до + 1, т.е. может быть отрицательным.

Гипотеза о значимости частного коэффициента корреляции проверяется так же, как и для парного коэффициента корреляции:

H₀ : t_r < t_таб(a; N-2)

3.4.4. Коэффициент детерминации

Коэффициент детерминации равен квадрату множественного коэффициента корреляции и показывает: какую долю общей дисперсии 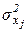исследуемого показателя Xj объясняет (формирует) вариация всех остальных (n-1) показателей X₁,X₂,…,X_n при их совместном действии:

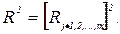(3.14)

3.4.5. Оценка значимости множественного коэффициента детерминации

Используется F – статистика Фишера для R²:

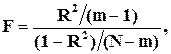(3.15)

где, m – число компонент вектора 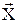; N – число опытов.

Проверяется нуль гипотеза:

H₀ : F = 0;

если 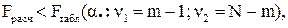то коэффициент множественной корреляции незначим (гипотеза Н₀ принимается);

если 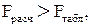то R² значим (гипотеза Н₀ отвергается);

– n₁– число степеней свободы для числителя; n₂ – число степеней свободы для знаменателя (n₁=m-1; n₂=N-m) дроби (2.15).

3.4.6. Индекс корреляции при нелинейной связи двух случайных величин

Слово «индекс» здесь понимается в смысле «отношения» [ ]. Поэтому употребляется и другой термин для этой числовой меры: «корреляционное отношение».

Пусть две случайные величины X и Y связаны в среднем нелинейным функциональным уравнением вида:

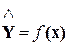(3.16)

Например:

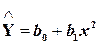
Функция f(x) должна быть априори известна.

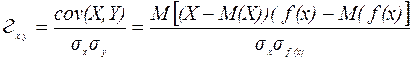(3.17)

Тогда выборочная оценка индекса корреляции равна:

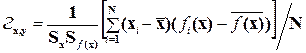(3.18)

Практическая формула для индекса корреляции:

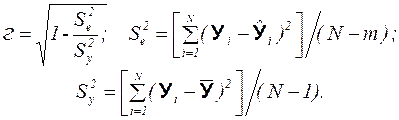(3.19)

Здесь:

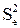– дисперсия остатков уравнения регрессии;

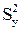– общая дисперсия как мера разброса наблюдений вокруг среднего.

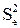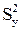Заметим, что при подстановке и под корень в уравнении (3.19) и условии (N-m)»(N-1) при больших N степени свободы 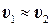и их можно сократить, откуда следует упрощенная приближенная расчетная формула.

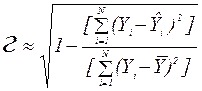(3.20)

Эта формула допускает наглядное толкование: чем сильнее стохастическая связь в уравнении (3.17), тем меньше доля дисперсии 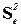по отношению к общей дисперсии 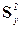и больше индекса корреляции .

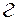3.4.7. Индекс множественной корреляции

Пусть построено нелинейное уравнение множественной регрессии:

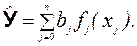(2.21)

Тогда использую простую формулу (2.21), можно получить индекс множественной корреляции

(2.22)

Соответственно квадрат этого индекса даст множественный индекс детерминации в нелинейном случае.