УМНОЖЕНИЕ ВЕКТОРА НА СКАЛЯР
Пусть даны вектор  и скаляр
и скаляр  . При умножении вектора
. При умножении вектора  на скаляр
на скаляр  модуль вектора
модуль вектора  изменяется в
изменяется в  раз, а его направление остаётся прежним или меняется на противоположное в зависимости от того, будет скаляр положительным или отрицательным числом. В результате такого действия образуется новый вектор ma, который называется произведением вектора
раз, а его направление остаётся прежним или меняется на противоположное в зависимости от того, будет скаляр положительным или отрицательным числом. В результате такого действия образуется новый вектор ma, который называется произведением вектора  на скаляр
на скаляр  , т.е.
, т.е. 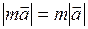 , где
, где  - абсолютная величина числа
- абсолютная величина числа  .
.
Введём понятие единичного вектора. Единичным вектором, или «ортом », направления  называется
называется 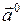 , имеющий направление вектора
, имеющий направление вектора  и модуль, равный единице:
и модуль, равный единице: 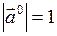 , тогда вектор
, тогда вектор  можно записать через единичный вектор следующим образом:
можно записать через единичный вектор следующим образом: 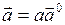 , где а – модуль вектора
, где а – модуль вектора  .
.
Любой вектор можно представить как произведение единичного вектора на модуль данного вектора. Например, дан вектор 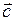 , пусть
, пусть 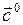 - единичный вектор, с – модуль вектора
- единичный вектор, с – модуль вектора 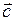 , тогда
, тогда 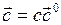 .
.
Проекция любого вектора, на какую либо ось равна его модулю, умноженному на косинус угла между положительным направлением оси проекции и направлением самого вектора. Из рисунка 5 следует, что
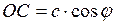 .
.

А теперь рассмотрим, что происходит в случае умножения вектора на положительный скаляр и на отрицательный скаляр.
Пусть у нас будут даны: вектор A и скаляр 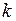 .
.
При умножении вектора A на положительный скаляр 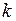 получаем новый вектор (
получаем новый вектор ( 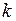 A), направление которого совпадает с направлением вектора A, а числовое значение отличается в
A), направление которого совпадает с направлением вектора A, а числовое значение отличается в 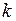 раз.
раз.
Пример 3: Определить импульс тела массой 2 кг, движущегося со скоростью 5 м/с.
Решение: Импульс тела равен: 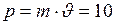 кг · м/с и направлен в сторону
кг · м/с и направлен в сторону 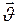 (рис.6).
(рис.6).

При умножении вектора A на отрицательный скаляр 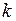 получаем новый вектор (
получаем новый вектор ( 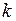 A), направление которого противоположно вектору A, а числовое значение отличается в
A), направление которого противоположно вектору A, а числовое значение отличается в 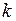 раз.
раз.
Пример 4: Заряд 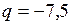 нКл помещён в электрическое поле с напряженностью
нКл помещён в электрическое поле с напряженностью 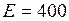 В/м. Найти модуль и направление силы, действующей на заряд.
В/м. Найти модуль и направление силы, действующей на заряд.
Решение: Сила, по определению, равна 
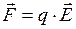 . Так как заряд отрицателен, то вектор силы направлен в сторону, противоположную
. Так как заряд отрицателен, то вектор силы направлен в сторону, противоположную 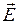 (рис.7). Модуль силы равен
(рис.7). Модуль силы равен 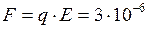 Н
Н 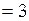 мкН.
мкН.

5. СКАЛЯРНОЕ ПРОИЗВЕДЕНИЕ ДВУХ ВЕКТОРОВ
Скалярным произведением двух векторов  и
и 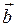 называется произведение их модулей на косинус угла между ними.
называется произведение их модулей на косинус угла между ними.
Скалярное произведение обозначается через ( 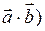 или
или 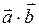 .
.
Итак, по определению скалярное произведение двух векторов  и
и 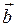 равно
равно
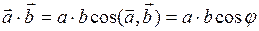 ,
,
где 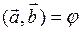 - угол между векторами
- угол между векторами  и
и 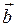 .
.
Скалярное произведение двух векторов есть скалярная величина, положительная или отрицательная, в зависимости от того, будет 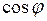 больше или меньше нуля, т.е. острый или тупой угол образуют векторы
больше или меньше нуля, т.е. острый или тупой угол образуют векторы  и
и 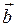 . Примером скалярного произведения является механическая работа
. Примером скалярного произведения является механическая работа 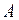 , равная произведению силы
, равная произведению силы 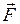 на вектор перемещения
на вектор перемещения 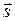 и косинус угла между ними, т.е.
и косинус угла между ними, т.е.
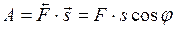 .
.
Если векторы параллельны, то скалярное произведение равно 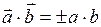 , так как
, так как 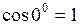 ;
; 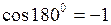 .
.
Если векторы перпендикулярны 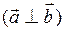 , то скалярное произведение векторов равно нулю:
, то скалярное произведение векторов равно нулю: 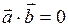 , так как
, так как 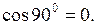
Пример5: Найти работу постоянной силы 20 Н, если перемещение тела 7,5 м , а угол 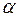 между силой и перемещением равен 1200.
между силой и перемещением равен 1200.
Решение: Работа силы равна, по определению, скалярному произведению силы и перемещения:
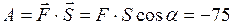 Дж
Дж
Дата добавления: 2016-09-06; просмотров: 11040;











