ОСНОВНЫЕ, ДОПОЛНИТЕЛЬНЫЕ И ПРОИЗВОДНЫЕ ЕДИНИЦЫ СИСТЕМЫ
I. ОСНОВНЫЕ ЕДИНИЦЫ
1. Метр(м) – это длина пути, проходимого светом в вакууме за промежуток времени 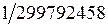 доли секунды. Из определения следует, что скорость света в вакууме принята равной
доли секунды. Из определения следует, что скорость света в вакууме принята равной 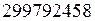 м/с точно. Современное определение метра в терминах времени и скорости света было введено в 1983г. До этого момента пользовались другим определением метра «Метр (м) – единица длины. Метр равен длине 1 650 763, 73 волн в вакууме излучения, соответствующего переходу между уровнями
м/с точно. Современное определение метра в терминах времени и скорости света было введено в 1983г. До этого момента пользовались другим определением метра «Метр (м) – единица длины. Метр равен длине 1 650 763, 73 волн в вакууме излучения, соответствующего переходу между уровнями 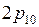 и
и 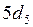 атома криптона – 86»
атома криптона – 86»
2. Килограмм (кг) – единица массы, равная массе международного прототипа килограмма. Из определения следует, что масса международного прототипа килограмма, всегда точно равна 1 кг.
3. Секунда (с) – интервал времени, равный 9 192 631 770 периодам излучения, соответствующего переходу между двумя сверхтонкими уровнями основного состояния атома цезия – 133. Из определения следует, что величина сверхтонкого расщепления основного состояния атома цезия – 133, равна 9 192 631 770 Гц точно.
II. ДОПОЛНИТЕЛЬНЫЕ ЕДИНИЦЫ
1. Радиан (рад) – единица плоского угла. Радиан равен углу между двумя радиусами окружности, длина дуги между которыми равна радиусу.
2. Стерадиан (ср) – единица телесного угла. Стерадиан равен телесному углу с вершиной в центре сферы, вырезающему на поверхности сферы площадь, равную площади квадрата со стороной, равной радиусу сферы.
III. ПРОИЗВОДНЫЕ ЕДИНИЦЫ МЕХАНИЧЕСКИХ ВЕЛИЧИН
Производные единицы Международной системы образуются из основных и дополнительных единиц при помощи определяющих уравнений.
Все производные единицы механических величин могут быть выражены через три основные единицы Международной системы – метр, килограмм, секунду и дополнительную единицу – радиан.
При построении системы единиц механических величин коэффициент пропорциональности во всех формулах принимается равным безразмерной единице.
А. ЕДИНИЦЫ ПРОСТРАНСТВА. ЕДИНИЦЫ ВЕЛИЧИН КИНЕМАТИКИ
Площадь. Единицу площади  найдём по формуле площади квадрата:
найдём по формуле площади квадрата:
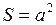 , (1)
, (1)
где 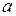 - длина его стороны. Положив
- длина его стороны. Положив 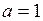 м, получим
м, получим 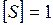 м2.
м2.
Квадратный метр равен площади квадрата со сторонами, длины которых равны 1 м.
Размерность площади 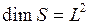 .
.
Объём. Вместимость. Единицу объёма 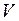 получим по формуле объёма куба:
получим по формуле объёма куба:
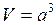 , (2)
, (2)
где 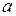 - длина его ребра. Положив в формуле (2)
- длина его ребра. Положив в формуле (2) 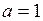 м, получим
м, получим 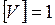 м3.
м3.
Кубический метр равен объёму куба с рёбрами, длины которых равны 1 м.
Размерность объёма 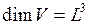 .
.
Скорость. Скорость – физическая величина, равная первой производной от перемещения по времени, т.е. 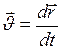 .
.
Для равномерного движения значение скорости может быть определено как отношение пути 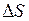 ко времени
ко времени  , за которое этот путь пройден:
, за которое этот путь пройден:
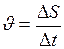 (3)
(3)
Положив в формуле (3) 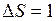 м,
м, 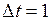 с, получим единицу скорости
с, получим единицу скорости 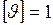 м/с. Эта единица носит название метр в секунду.
м/с. Эта единица носит название метр в секунду.
Метр в секунду равен скорости прямолинейно и равномерно движущейся точки, при которой эта точка за время 1с перемещается на расстояние 1м.
Размерность скорости: 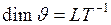 .
.
Ускорение. Ускорением называют физическую величину, равную первой производной от скорости по времени, т.е. 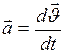 .
.
В случае равнопеременного движения, для которого ускорение есть величина постоянная, оно может быть определено по формуле:
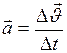 , (4)
, (4)
где 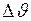 - изменение скорости равнопеременного движения за время
- изменение скорости равнопеременного движения за время  . Положив в формулу (4)
. Положив в формулу (4) 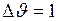 м/с,
м/с, 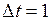 с, получим
с, получим 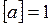 м/с2. Эта единица называется метр на секунду в квадрате.
м/с2. Эта единица называется метр на секунду в квадрате.
Метр на секунду в квадрате равен ускорению прямолинейно и равноускоренно движущейся точки, при котором за время 1 с скорость точки возрастает на 1 м/с.
Размерность ускорения: 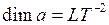 .
.
Период. Период – это время, в течение которого совершается один цикл периодического процесса (колебаний, излучений и т.п.) или одно дискретное событие (импульс, удар и т.п.).
Период 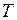 выражается в единицах времени (в СИ – в секундах).
выражается в единицах времени (в СИ – в секундах).
Частота. Следует различать частоту периодического процесса (колебаний, излучений и т.п.), частоту дискретных событий (импульсов и т.д.) и частоту вращения.
Частотой 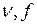 периодического процесса называют физическую величину, равную числу циклов, происходящих за единицу времени. Из этого определения следует, что частота есть величина, обратная периоду, т.е.:
периодического процесса называют физическую величину, равную числу циклов, происходящих за единицу времени. Из этого определения следует, что частота есть величина, обратная периоду, т.е.:
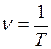 (5)
(5)
Положив в формулу (5) 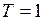 с, найдём
с, найдём 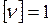 с-1. Эта единица называется герцем (Гц).
с-1. Эта единица называется герцем (Гц).
Герц равен частоте периодического процесса, при которой за время 1 с происходит один цикл периодического процесса.
Частотой 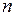 дискретных событий называют физическую величину, равную числу событий, происходящих в единицу времени. Частота дискретных событий и время
дискретных событий называют физическую величину, равную числу событий, происходящих в единицу времени. Частота дискретных событий и время 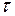 , затрачиваемое на одно событие, связаны соотношением:
, затрачиваемое на одно событие, связаны соотношением:
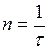 (6)
(6)
Из формулы (6) следует, что единица дискретных событий: 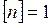 с-1. Эта единица называется секунда в минус первой степени.
с-1. Эта единица называется секунда в минус первой степени.
Секунда в минус первой степени равна частоте вращения, при которой за 1с происходит один цикл вращения (один оборот).
Размерность частоты: 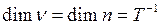 .
.
Кривизна. Кривизна кривой характеризует степень отличия её от прямой. В общем случае кривизна кривой в разных её точках различна, и только кривизна окружности во всех её точках одна и та же.
Кривизна 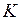 кривой в некоторой её точке есть величина, обратная радиусу
кривой в некоторой её точке есть величина, обратная радиусу 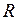 кривизны, т.е.:
кривизны, т.е.:
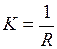 (7)
(7)
Радиус кривизны – это радиус соприкасающейся окружности. Для получения единицы кривизны положим в формуле (7) 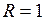 м. Тогда
м. Тогда 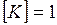 м-1. Эта единица называется метр в минус первой степени.
м-1. Эта единица называется метр в минус первой степени.
Размерность кривизны: 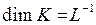 .
.
Угловая скорость. Угловой скоростью 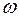 называют физическую величину, равную первой производной от угла поворота тела по времени, т.е.:
называют физическую величину, равную первой производной от угла поворота тела по времени, т.е.: 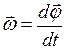 .
.
При равномерном вращательном движении тела угловая скорость – эта величина, равная отношению угла поворота 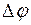 к интервалу времени
к интервалу времени  , за которое произошёл этот поворот:
, за которое произошёл этот поворот:
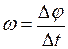 (8)
(8)
Положив в формулу (8) 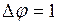 рад,
рад, 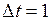 с, получим
с, получим 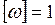 рад/с.
рад/с.
Радиан в секунду равен угловой скорости равномерновращающегося тела, при которой за время 1 с совершается поворот тела относительно оси вращения на угол 1 рад.
Так как плоский угол является не основной, а дополнительной величиной Международной системы, то в размерность производных величин он не входит. Учитывая это, из формулы (8) найдём размерность угловой скорости: 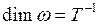 .
.
Угловое ускорение. Угловым ускорением называют физическую величину, определяемую первой производной от угловой скорости по времени: 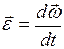 .
.
При равноускоренном вращении тела угловое ускорение есть величина, равная отношению изменения 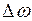 угловой скорости ко времени
угловой скорости ко времени  , в течение, которого произошло это изменение:
, в течение, которого произошло это изменение:
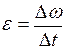 (9)
(9)
Положив в формулу (9) 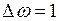 рад/с,
рад/с, 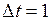 с, получим:
с, получим: 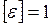 рад/с2.
рад/с2.
Радиан на секунду в квадрате равен угловому ускорению равноускоренно вращающегося тела, при котором за время 1 с угловая скорость тела возрастает на 1 рад/с.
Размерность углового ускорения: 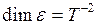 .
.
B. ЕДИНИЦЫ ВЕЛИЧИН ДИНАМИКИ
Сила. Сила – это векторная величина, являющаяся мерой механического воздействия на тело со стороны других тел или полей. Единицу силы 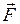 найдём по формуле, выражающей второй закон Ньютона:
найдём по формуле, выражающей второй закон Ньютона:
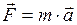 , (10)
, (10)
где  - масса тела,
- масса тела,  - ускорение, сообщаемое этому телу силой
- ускорение, сообщаемое этому телу силой 
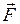 . Положив в формулу (10)
. Положив в формулу (10) 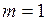 кг,
кг, 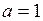 м/с2, получим:
м/с2, получим: 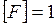 кг·м/с2. Эта единица носит название Ньютон (Н).
кг·м/с2. Эта единица носит название Ньютон (Н).
Ньютон равен силе, сообщающей телу массой 1 кг ускорение 1 м/с2 в направлении действия силы.
В Ньютонах выражается также вес тела 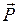 . Вес тела – это сила, с которой тело действует на опору или подвес. В случае если опора или подвес не имеют ускорения в вертикальном направлении, вес тела связан с его массой соотношением:
. Вес тела – это сила, с которой тело действует на опору или подвес. В случае если опора или подвес не имеют ускорения в вертикальном направлении, вес тела связан с его массой соотношением: 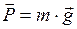 , где
, где 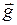 - ускорение свободного падения.
- ускорение свободного падения.
Размерность силы, а, следовательно, и веса: 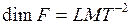 .
.
Плотность. Плотностью 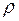 вещества называют физическую величину, определяемую отношением:
вещества называют физическую величину, определяемую отношением: 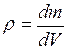 .
.
В случае однородного тела плотность
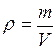 , (11)
, (11)
где  - масса тела,
- масса тела, 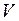 - его объём. Положив в формулу (11)
- его объём. Положив в формулу (11) 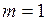 кг,
кг, 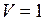 м3, получим единицу плотности:
м3, получим единицу плотности: 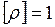 кг/м3.
кг/м3.
Килограмм на кубический метр равен плотности однородного вещества, масса которого при объёме 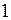 м3 равна
м3 равна 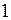 кг.
кг.
Размерность плотности: 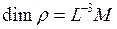 .
.
Относительная плотность. Относительной величиной называют величину, равную безразмерному отношению физической величины к одноимённой величине, принимаемой за исходную.
Все относительные величины выражаются в безразмерных единицах. Безразмерная единица равна относительной величине, равной 1.
Относительной плотностью вещества называют величину, равную отношению его плотности к плотности некоторого вещества при определённых физических условиях. Таким стандартным веществом является вода при температуре 3,980С и нормальном атмосферном давлении (101 325 Па) или сухой воздух при 20 0С и нормальном атмосферном давлении.
Относительная плотность:
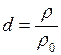 , (12)
, (12)
где 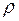 - плотность данного вещества,
- плотность данного вещества, 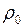 - плотность стандартного вещества.
- плотность стандартного вещества.
Положив в формуле (12) 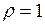 кг/м3;
кг/м3; 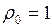 кг/м3, получим единицу относительной плотности:
кг/м3, получим единицу относительной плотности: 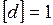 . Следовательно, относительная плотность выражается в безразмерных единицах.
. Следовательно, относительная плотность выражается в безразмерных единицах.
Удельный объём. Удельным объёмом называют величину, равную отношению объёма 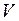 тела к его массе
тела к его массе  :
:
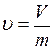 (13)
(13)
Положив 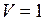 м3;
м3; 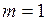 кг, получим единицу удельного объёма:
кг, получим единицу удельного объёма: 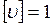 м3/кг.
м3/кг.
Кубический метр на килограмм равен удельному объёма однородного вещества, объём которого при массе 1 кг равен 1 м3.
Размерность удельного объёма: 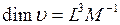 .
.
Из сравнения формул (11) и (13), а также размерностей удельного объёма и плотности следует, что удельный объём есть величина, обратная плотности.
Удельный вес. Удельным весом тела называют физическую величину, определяемую соотношением: 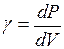 .
.
Для однородного тела:
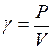 , (14)
, (14)
где 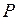 - вес тела,
- вес тела, 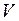 - его объём. Положив в (14)
- его объём. Положив в (14) 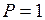 Н,
Н, 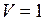 м3, получим единицу удельного веса:
м3, получим единицу удельного веса: 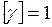 Н/м3.
Н/м3.
Ньютон на кубический метр равен удельному весу однородного вещества, вес которого при объёме 1м3 равен 1Н.
Размерность удельного веса: 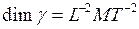 .
.
Давление. Давлением 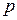 называют физическую величину, равную отношению силы
называют физическую величину, равную отношению силы 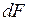 , действующей на элемент поверхности нормально к ней, к площади
, действующей на элемент поверхности нормально к ней, к площади 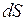 этого элемента, т.е.
этого элемента, т.е. 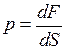 .
.
При равномерном распределении силы 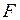 по поверхности площадью
по поверхности площадью  давление выражается формулой:
давление выражается формулой:
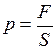 (15)
(15)
Положив 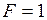 Н,
Н, 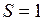 м2, получим единицу давления:
м2, получим единицу давления: 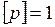 Н/м2.
Н/м2.
Эта единица называется паскаль (Па). Паскаль равен давлению, вызываемому силой 1Н, равномерно распределённой по нормальной поверхности площадью 1м2.
Размерность давления: 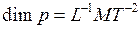 .
.
Импульс (количество движения). Импульсом 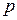 тела называют величину, равную произведению массы тела на его скорость, т.е.
тела называют величину, равную произведению массы тела на его скорость, т.е.
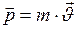 (16)
(16)
Положив 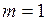 кг,
кг, 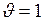 м/с, получим единицу импульса:
м/с, получим единицу импульса: 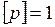 кг·м/с.
кг·м/с.
Килограмм – метр в секунду равен импульсу (количеству движения) тела массой 1 кг, движущегося поступательно со скоростью 1 м/с.
Размерность импульса: 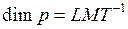 .
.
Импульс силы. Импульсом силы 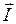 называют физическую величину, равную произведению вектора силы на время её действия, т.е.
называют физическую величину, равную произведению вектора силы на время её действия, т.е.
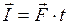 (17)
(17)
Положив 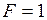 Н,
Н, 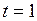 с, получим единицу импульса силы:
с, получим единицу импульса силы: 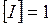 Н∙с.
Н∙с.
Ньютон-секунда равен импульсу силы, действующей в течение времени 1с.
Размерность импульса силы: 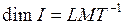 . Сравнив размерности импульса силы и импульса, видим, что они одинаковы. Это следует и из второго закона Ньютона:
. Сравнив размерности импульса силы и импульса, видим, что они одинаковы. Это следует и из второго закона Ньютона: 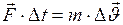 .
.
Работа, механическая энергия. Работой 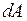 называют величину, равную скалярному произведению силы
называют величину, равную скалярному произведению силы 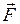 на бесконечно малое перемещение
на бесконечно малое перемещение 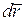 тела под действием этой силы:
тела под действием этой силы: 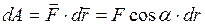 .
.
При прямолинейном движении тела на пути 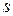 под действием постоянной силы
под действием постоянной силы 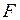 работа определяется по формуле:
работа определяется по формуле:
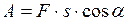 , (18)
, (18)
где 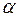 - угол между направлениями действия силы и движения тела.
- угол между направлениями действия силы и движения тела.
Положив в (18) 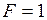 Н,
Н, 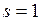 м,
м, 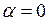 , получим:
, получим: 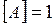 Н∙м. Эта единица называется джоуль (Дж). Джоуль равен работе, совершаемой при перемещении точки приложения силы 1Н на расстоянии 1м в направлении действия силы.
Н∙м. Эта единица называется джоуль (Дж). Джоуль равен работе, совершаемой при перемещении точки приложения силы 1Н на расстоянии 1м в направлении действия силы.
Размерность работы: 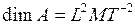 .
.
Кинетическая энергия. Кинетической энергией 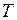 называют энергию движущегося тела и определяют по формуле:
называют энергию движущегося тела и определяют по формуле:
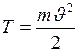 , (19)
, (19)
где  - масса тела,
- масса тела, 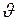 - его скорость.
- его скорость.
Положив в (19) 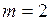 кг,
кг, 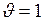 м/с2, найдём единицу кинетической энергии:
м/с2, найдём единицу кинетической энергии: 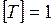 кг·м·с-2 = 1Дж. Следовательно, кинетическая энергия выражается в тех же единицах, что и работа, т.е. в джоулях. Размерность кинетической энергии:
кг·м·с-2 = 1Дж. Следовательно, кинетическая энергия выражается в тех же единицах, что и работа, т.е. в джоулях. Размерность кинетической энергии: 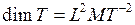 .
.
Потенциальная энергия. Потенциальной энергией 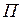 называют энергию взаимодействия тел. Единицу этой энергии определим по формуле потенциальной энергии тела массой
называют энергию взаимодействия тел. Единицу этой энергии определим по формуле потенциальной энергии тела массой  , поднятого над Землёй на высоту
, поднятого над Землёй на высоту 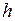 над её поверхностью:
над её поверхностью:
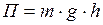 (20)
(20)
Положив 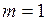 кг,
кг, 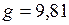 м/с2,
м/с2, 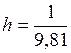 м, найдём единицу потенциальной энергии:
м, найдём единицу потенциальной энергии: 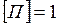 кг∙м·с2
кг∙м·с2 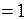 Дж. Следовательно, потенциальная энергия выражается в джоулях.
Дж. Следовательно, потенциальная энергия выражается в джоулях.
Размерность потенциальной энергии: 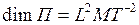 .
.
Коэффициент полезного действия. Коэффициент полезного действия 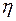 - относительная величина, равная отношению полезно использованной энергии
- относительная величина, равная отношению полезно использованной энергии 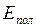 к суммарной энергии
к суммарной энергии 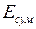 , полученной системой, т.е.
, полученной системой, т.е. 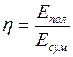 .
.
Положив 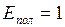 Дж,
Дж, 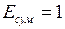 Дж, получим единицу коэффициента полезного действия:
Дж, получим единицу коэффициента полезного действия: 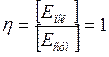 .
.
Следовательно, коэффициент полезного действия, как и любая относительная величина, выражается в безразмерных единицах.
Мощность. Мощность есть физическая величина, равная отношению работы 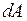 к бесконечно малому промежутку времени
к бесконечно малому промежутку времени 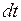 , в течение которого эта работа совершается:
, в течение которого эта работа совершается: 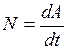 .
.
В случае постоянной мощности формула принимает вид:
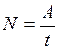 (21)
(21)
Положив 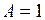 Дж,
Дж, 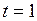 с, получим единицу мощности:
с, получим единицу мощности: 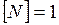 Дж/с. Эта единица носит название ватт (Вт). Ватт равен мощности, при которой за время 1с совершается работа в 1 Дж.
Дж/с. Эта единица носит название ватт (Вт). Ватт равен мощности, при которой за время 1с совершается работа в 1 Дж.
Размерность мощности: 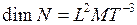 .
.
Момент силы. Моментом силы 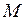 относительно некоторой точки называют векторную физическую величину, равную произведению радиус-вектора, проведенного от оси вращения к точке приложения силы, на вектор этой силы.
относительно некоторой точки называют векторную физическую величину, равную произведению радиус-вектора, проведенного от оси вращения к точке приложения силы, на вектор этой силы.
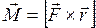 (22)
(22)
Подставив 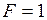 Н,
Н, 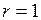 м, получим единицу момента силы:
м, получим единицу момента силы: 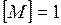 Н·м.
Н·м.
Ньютон – метр равен моменту силы, создаваемому силой 1Н относительно точки, расположенной на расстоянии 1м от линии действия силы.
Размерность момента силы: 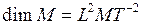 .
.
Момент инерции (динамический момент инерции). Моментом инерции 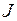 тела относительно некоторой оси вращения называют величину, равную сумме произведений масс всех частиц тела на квадраты их расстояний от этой оси. Единицу момента инерции удобно определить по формуле момента инерции удобно определить по формуле момента инерции материальной точки относительно некоторой оси вращения:
тела относительно некоторой оси вращения называют величину, равную сумме произведений масс всех частиц тела на квадраты их расстояний от этой оси. Единицу момента инерции удобно определить по формуле момента инерции удобно определить по формуле момента инерции материальной точки относительно некоторой оси вращения:
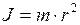 , (23)
, (23)
где  - масса материальной точки,
- масса материальной точки, 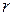 - расстояние её до оси инерции.
- расстояние её до оси инерции.
Положив в (23) 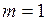 кг,
кг, 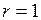 м, получим единицу момента инерции:
м, получим единицу момента инерции: 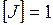 кг∙м2.
кг∙м2.
Килограмм - метр в квадрате равен моменту инерции материальной точки массой 1 кг, находящейся на расстоянии 1м от оси инерции.
Размерность момента инерции: 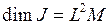 .
.
Момент импульса (момент количества движения). Моментом импульса 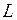 тела называют величину, равную произведению момента инерции
тела называют величину, равную произведению момента инерции 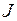 тела на его угловую скорость
тела на его угловую скорость 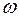 :
:
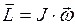 (24)
(24)
Момент импульса тела равен сумме моментов импульса всех его частиц (материальных точек).
Момент импульса материальной точки относительно некоторой точки (полюса) есть произведение длины радиуса - вектора 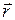 материальной точки, проведённого из полюса, на её импульс, т.е.
материальной точки, проведённого из полюса, на её импульс, т.е.
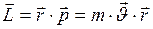 , (25)
, (25)
где 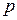 - импульс материальной точки,
- импульс материальной точки,  и
и 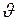 - её масса и скорость.
- её масса и скорость.
Подставив в (25) 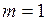 кг,
кг, 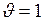 м/с
м/с 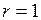 м, получим единицу момента импульса:
м, получим единицу момента импульса: 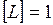 кг∙м2/с.
кг∙м2/с.
Килограмм-метр в квадрате в секунду равен моменту импульса (моменту количества движения) тела с моментом инерции 1кг∙м2, вращающегося с угловой скоростью 1 рад/с. Единица момента импульса получена по формуле (25), а определение единицы дано на основе формулы (24). Обе указанные формулы дают одинаковую размерность момента импульса: 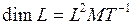 .
.
Относительное удлинение. Относительным удлинением 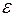 называют величину, равную отношению абсолютного удлинения
называют величину, равную отношению абсолютного удлинения 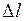 тела к первоначальной его длине
тела к первоначальной его длине 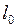 :
:
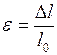 (26)
(26)
Подставив 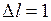 м,
м, 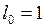 м, найдём единицу относительного удлинения:
м, найдём единицу относительного удлинения: 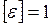 . Относительное удлинение выражается в безразмерных единицах. В безразмерных единицах выражаются также другие виды относительной деформации: относительное поперечное сжатие, относительный сдвиг и т.д.
. Относительное удлинение выражается в безразмерных единицах. В безразмерных единицах выражаются также другие виды относительной деформации: относительное поперечное сжатие, относительный сдвиг и т.д.
Нормальное механическое напряжение (нормальное напряжение). Нормальным напряжением 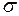 называют физическую величину, равную отношению упругой силы к площади перпендикулярного силе сечения тела, т.е.:
называют физическую величину, равную отношению упругой силы к площади перпендикулярного силе сечения тела, т.е.: 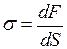 .
.
При равномерном распределении напряжения оно может быть выражено формулой:
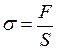 (27)
(27)
Подставив 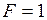 Н,
Н, 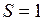 м2, получим единицу нормального напряжения:
м2, получим единицу нормального напряжения: 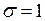 Н/м2. Напряжение выражается в тех же единицах, что и давление, т.е. в паскалях.
Н/м2. Напряжение выражается в тех же единицах, что и давление, т.е. в паскалях.
В паскалях выражаются касательное напряжение и все критические значения напряжений: предел пропорциональности 
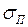 , предел текучести
, предел текучести 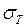 , предел прочности
, предел прочности 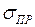 и другие.
и другие.
Размерность напряжения: 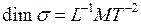 .
.
Модуль упругости. Модуль упругости – величина, равная отношению напряжения к относительному удлинению.
Единицу модуля упругости 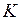 найдём по закону Гука:
найдём по закону Гука:
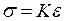 (28)
(28)
Так как 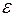 - безразмерная величина, то модуль упругости, как это следует из формулы (28), выражается в тех же единицах, что и напряжение, т.е. в паскалях, и имеет ту же размерность:
- безразмерная величина, то модуль упругости, как это следует из формулы (28), выражается в тех же единицах, что и напряжение, т.е. в паскалях, и имеет ту же размерность: 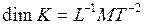 .
.
Модуль Юнга (модуль продольной упругости). Для случая продольной деформации (линейного растяжения или сжатия) закон Гука имеет вид:
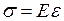 , (29)
, (29)
где Е – модуль Юнга. Он равен тому напряжения, при котором относительное удлинение равно единице, а абсолютное удлинение – первоначальной длине. Из этого определения, а также из формулы (29) следует, что единицей модуля Юнга является паскаль, а его размерность: 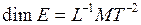 .
.
Коэффициент Пуассона. При продольном растяжении образца происходит уменьшение его поперечных размеров, которое характеризуется абсолютным 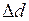 и относительным
и относительным 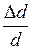 сжатиями, где
сжатиями, где 
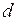 - поперечный размер образца. Отношение относительного сжатия к относительному удлинению называют коэффициентом Пуассона
- поперечный размер образца. Отношение относительного сжатия к относительному удлинению называют коэффициентом Пуассона 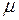 :
:
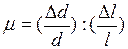 (30)
(30)
Так как 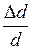 и
и 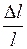 - величины безразмерные, то и коэффициент Пуассона – величина безразмерная и, следовательно, выражается в безразмерных единицах.
- величины безразмерные, то и коэффициент Пуассона – величина безразмерная и, следовательно, выражается в безразмерных единицах.
Модуль сдвига. Модулем сдвига 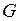 называют модульупругости для деформации сдвига. Он равен отношению касательного напряжения
называют модульупругости для деформации сдвига. Он равен отношению касательного напряжения 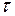 к деформации сдвига (углу сдвига)
к деформации сдвига (углу сдвига) 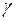 :
: 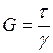 .
.
Модуль сдвига, модуль Юнга и коэффициент Пуассона связаны соотношением:
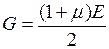 (31)
(31)
Отсюда следует, что модуль сдвига выражается в тех же единицах, что и модуль Юнга, т.е. в паскалях, и имеет размерность: 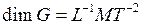 .
.
Жёсткость. Жёсткость – величина, равная отношению упругой силы 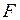 , возникающей в теле при его растяжении, к абсолютной деформации
, возникающей в теле при его растяжении, к абсолютной деформации 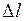 . Жёсткость
. Жёсткость 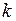 является коэффициентом пропорциональности в законе Гука, записанном в виде:
является коэффициентом пропорциональности в законе Гука, записанном в виде: 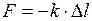 . Из этой формулы получим:
. Из этой формулы получим:
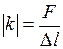 (32)
(32)
Положив 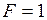 Н,
Н, 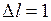 м, найдём единицу жёсткости:
м, найдём единицу жёсткости: 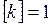 Н/м.
Н/м.
Ньютон на метр равен жёсткости тела, в котором возникает упругая сила 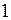 Н при абсолютном удлинении этого тела на 1м.
Н при абсолютном удлинении этого тела на 1м.
Размерность жёсткости: 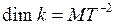 .
.
Коэффициент трения скольжения. Коэффициент трения скольжения 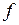 есть коэффициент пропорциональности между силой
есть коэффициент пропорциональности между силой 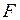 трения скольжения и силой
трения скольжения и силой 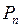 нормального давления. Из формулы силы трения:
нормального давления. Из формулы силы трения: 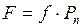 , получим:
, получим:
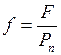 (33)
(33)
Положив 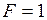 Н,
Н, 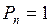 Н, найдём единицу трения скольжения:
Н, найдём единицу трения скольжения: 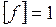 , т.е. коэффициент трения – величина безразмерная и выражается в безразмерных единицах.
, т.е. коэффициент трения – величина безразмерная и выражается в безразмерных единицах.
Коэффициент трения качения. Сила 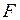 трения качения определяется по закону Кулона:
трения качения определяется по закону Кулона: 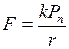 , где
, где 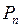 - сила нормального давления;
- сила нормального давления; 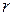 - радиус катящегося тела (круглого цилиндра, шара);
- радиус катящегося тела (круглого цилиндра, шара); 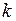 - коэффициент трения качения. Отсюда
- коэффициент трения качения. Отсюда
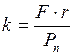 (34)
(34)
Положив здесь 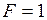 Н,
Н, 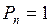 Н,
Н, 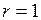 м, получим единицу коэффициента трения качения:
м, получим единицу коэффициента трения качения: 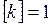 м. Следовательно, коэффициент трения качения выражается в метрах и имеет размерность:
м. Следовательно, коэффициент трения качения выражается в метрах и имеет размерность: 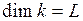 .
.
Напряжённость гравитационного поля. Напряжённостью 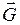 гравитационного поля называют векторную физическую величину, характеризующую гравитационное поле в данной точке и численно равную отношению вектора силы тяготения
гравитационного поля называют векторную физическую величину, характеризующую гравитационное поле в данной точке и численно равную отношению вектора силы тяготения 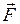 , действующей на тело, помещённое в данную точку поля, к гравитационной массе этого тела
, действующей на тело, помещённое в данную точку поля, к гравитационной массе этого тела  , т.е.
, т.е.
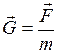 (35)
(35)
Положив 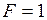 Н,
Н, 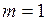 кг, получим единицу напряжённости гравитационного поля:
кг, получим единицу напряжённости гравитационного поля: 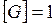 Н/кг.
Н/кг.
Ньютон на килограмм равен напряжённости гравитационного поля, которое на материальную точку массой 1 кг действует с силой 1Н.
Размерность напряжённости гравитационного поля: 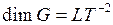 .
.
Следовательно, напряжённость гравитационного поля имеет размерность ускорения.
Потенциал гравитационного поля. Потенциалом 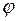 гравитационного поля называют физическую величину, равную отношению потенциальной энергии
гравитационного поля называют физическую величину, равную отношению потенциальной энергии 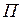 , которой обладает в гравитационном поле материальная точка, к массе
, которой обладает в гравитационном поле материальная точка, к массе  этой точки, т.е.
этой точки, т.е.
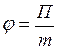 (36)
(36)
Положив 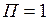 Дж,
Дж, 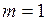 кг, получим единицу потенциала гравитационного поля:
кг, получим единицу потенциала гравитационного поля: 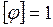 Дж/кг.
Дж/кг.
Джоуль на килограмм равен потенциалу гравитационного поля, в котором материальная точка массой 1 кг обладает потенциальной энергией 1Дж.
Размерность потенциала гравитационного поля: 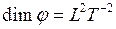 .
.
Таблица I.1 Множители и приставки для образования десятичных кратных и дольных единиц и их наименований
| Множитель | Приставка | ||
| Наименование | Обозначение | ||
| русское | международное | ||
| 1 000 000 000 000 000 000=1018 | экса | Э | Е |
| 1 000 000 000 000 000 = 1015 | пэта | П | Р |
| 1 000 000 000 000 = 1012 | тера | Т | Т |
| 1 000 000 000 = 109 | гига | Г | G |
| 1 000 000 = 106 | мега | М | М |
| 1 000 = 103 | кило | к | k |
| 100 = 102 | (гекто) | г | h |
| 10 = 101 | (дека) | да | da |
| 0,1 = 10-1 | (деци) | д | d |
| 0,01 = 10-2 | (санти) | с | с |
| 0,001 = 10-3 | милли | м | m |
| 0,000 001 = 10-6 | микро | мк | 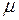
|
| 0,000 000 001 = 10-9 | нано | н | n |
| 0,000 000 000 001= 10-12 | пико | п | p |
| 0, 000 000 000 000 001 = 10-15 | фемто | ф | f |
| 0,000 000 000 000 000 001=1018 | атто | а | а |
Примечание: В скобках указаны приставки, которые допускаются применять только в наименованиях кратных и дольных единиц, уже получивших широкое распространение (например: дециметр, сантиметр).
Таблица I.2 Универсальные физические постоянные
| № | Величина | Обозначение | Числовое значение и ед.измерения в СИ |
| Радиус Земли | R | 6,37∙106 м | |
| Масса Земли | М | 5,97∙1024 кг | |
| Нормальное ускорение свободного падения | 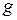
| 9,8 м/с2 | |
| Гравитационная постоянная | 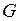
| 6,67∙1011 м3/(кг∙с2) | |
| Скорость света в вакууме | 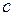
| 3∙108 м/с |
Таблица I.3 Единицы величин пространства и времени. Единицы механических величин
| Величина | Единица СИ | |||
| наименование | размерность | определяющее уравнение | наименование | обозначение |
| Длина | L
Дата добавления: 2016-09-06; просмотров: 2853; |











