Восстановление скалярного поля j по заданному градиенту этого поля

Допустим, что имеет место соотношение

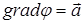, (1)

в каждой точке произвольной области S изменения пространственных переменных. Соотношение (1) имеет смысл только в том случае, если 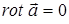, (x,y,z) 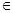S. Считаем, что это ограничение выполнено. В этом случае задача восстановления скалярного поля j по заданному векторному полю его градиента решается вычислением выражения

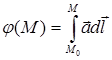, (2)

где дуга М₀М является произвольной.

Условие однозначной разрешимости рассматриваемой задачи состоит в требовании непрерывности вектора 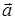и его первых частных производных, кроме того, область изменения переменных S должна быть односвязной.

При решении рассматриваемой задачи необходимо помнить, что восстановить поле j принципиально возможно с точностью до произвольной постоянной. Так, в формуле (2) неявно предполагается, что j(M₀)=0. Это ограничение в физике не является существенным, т.к. физический смысл имеет разность j(M) - j(M₀) значений скалярного поля в различных точках (разность потенциалов).