Вывод расчетных формул контактных напряжений в очаге деформации с одним нейтральным сечением

В дифференциальном уравнении равновесия (6.29) содержатся 3 неизвестных: p_x, σ_x, τ_x.

Для дальнейшего преобразования его к виду, пригодному для решения, используем остальные два уравнения: уравнение упругости (6.23) и уравнение, связывающее напряжения τ_x и p_x по закону трения скольжения.

Из уравнения упругости (6.23) выразим σ_x через p_x:

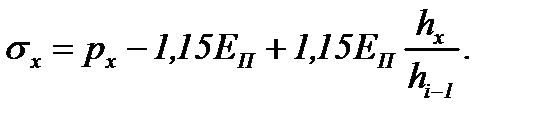(6.30)

Откуда: 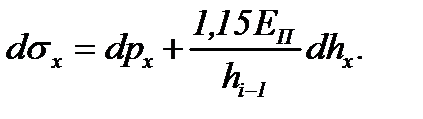(6.31)

Подставив τ_x из формулы (6.21), σ_x и dσ_x из формул (6.30), (6.31) в уравнение (6.29) и введя обозначение:

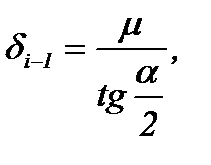(6.32)

окончательно получим дифференциальное уравнение, выражающее зависимость напряжения p_x от толщины h_x:

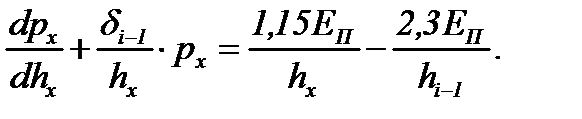(6.33)

Это уравнение представляет собой линейное дифференциальное уравнение 1-го порядка стандартного вида:

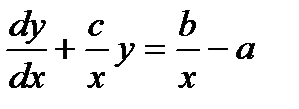, (6.34)

связывающее независимую переменную x(x=h_x) и зависящую от нее функцию y(y = p_x).

В теории дифференциальных уравнений известен метод решения уравнений типа (6.34) (путем подстановки y=u·v, где u и v – вспомогательные функции). Применив этот метод, получим общее решение уравнения (6.33):

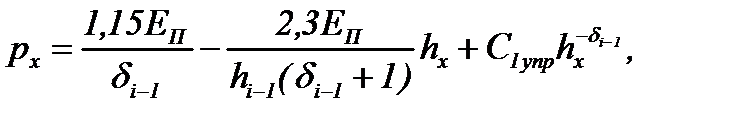(6.35)

где δ_i-1 – коэффициент, определяемый по формуле (6.32), пропорциональный коэффициенту трения μ;

C_1упр – постоянная интегрирования, которая определяется из граничных условий на входе в очаг деформации: при h_x=h_i-1, σ_x=- σ_i-1 (удельное натяжение полосы на входе в i-ю клеть). Подстановка этих значений h_x и σ_x в уравнение упругости (6.23) дает значение p_x на входе в очаг деформации: p_x=- σ_i-1.

Подставив эти граничные условия в общее решение (6.35), нашли постоянную интегрирования С_1упр, в результате получили окончательное выражение p_x(h_x) на первом упругом участке очага деформации:

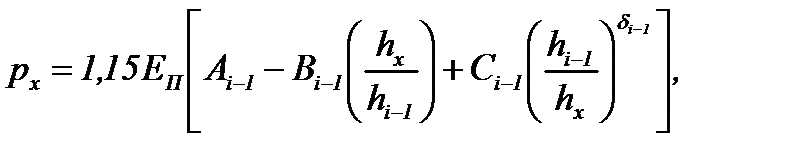(6.36)

где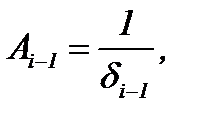

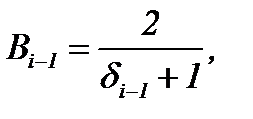
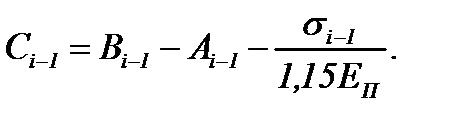
Аналогичный алгоритм используют при выводе формулы p_x(h_x) для остальных участков очага деформации, соблюдая такую последовательность: 1-й упругий участок – зона отставания пластического участка – 2-й упругий участок (если он полностью находится в зоне опережения, т.е. второе нейтральное сечение отсутствует) – зона опережения пластического участка.

Эта последовательность позволяет находить постоянные интегрирования для общих решений дифференциальных уравнений p_x(h_x): получив решение p_x(h_x) для первого упругого участка (выражение (6.36)), подставляют в него значения толщины полосы на границе с зоной отставания: h_x=h_1упр (см. рис. 6.2,а).

Полученное значение p_x(h_1упр) используют в качестве граничного условия в общем решении уравнения p_x(h_x) для зоны отставания пластического участка, находя соответствующую постоянную интегрирования. Затем решают дифференциальное уравнение p_x(h_x) для второго упругого участка, используя в качестве граничных условий толщину полосы на выходе из очага деформации h_x=h_i и переднее натяжение полосы: σ_x(h_i)=- σ_i.

Получив таким образом окончательное выражение p_x(h_x) для второго упругого участка, подставляют в него значение p_x(h_x=h_min) на границе с зоной опережения пластического участка, использовав полученное значение в качестве граничного условия в общем решении дифференциального уравнения p_x(h_x) для зоны опережения пластического участка.

Необходимые для описанного решения значения толщины полосы на границах упругих участков, согласно формулам (6.13) и (6.15), равны (см. рис. 6.2,а):

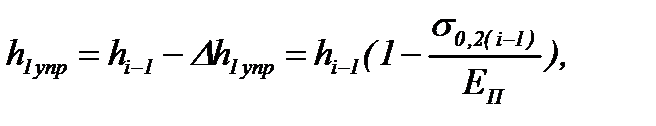(6.37)

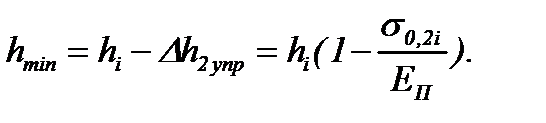(6.38)

Окончательные формулы p_x(h_x) для всех участков очага деформации с одним нейтральным сечением приведены в таблице 6.3.

Вычислив по этим формулам p_x(h_x), легко определить и остальные контактные напряжения: касательные τ_x по формуле (6.21); сжимающие σ_x – с помощью формул (6.23), (6.24) или (6.25).

Детальный анализ формул таблицы 6.3 изложен ниже, в п. 6.4 этой главы.

Предварительный их анализ позволяет сделать следующие выводы.

1. На упругих участках очага деформации контактные напряжения пропорциональны модулю упругости материала полосы Е_п и не зависит от предела текучести.

2. На пластических участках контактные напряжения пропорциональны пределу текучести полосы σ_ф2i и, кроме того, находятся в сложной зависимости от отношения Е_п/σ_ф2i, через которое на напряжения в пластической области проявляется влияние напряженного состояния упругих участков.

Таблица 6.3

Формулы p_x(h_x) для очага деформации с одним нейтральным сечением

Участок	Формула px(hx)	Формулы коэффициентов
Первый упругий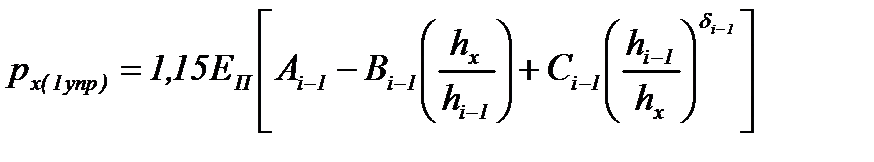
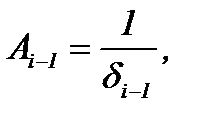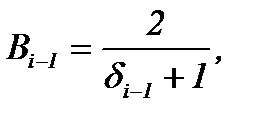
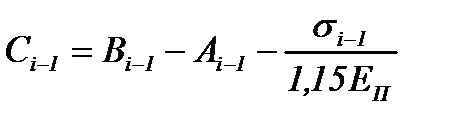
Второй упругий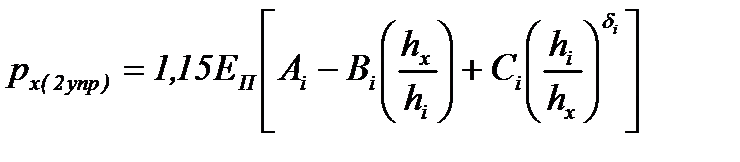
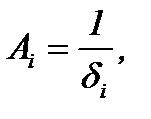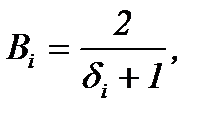
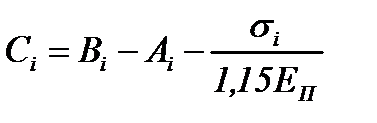
Пластичес-кий – зона отставания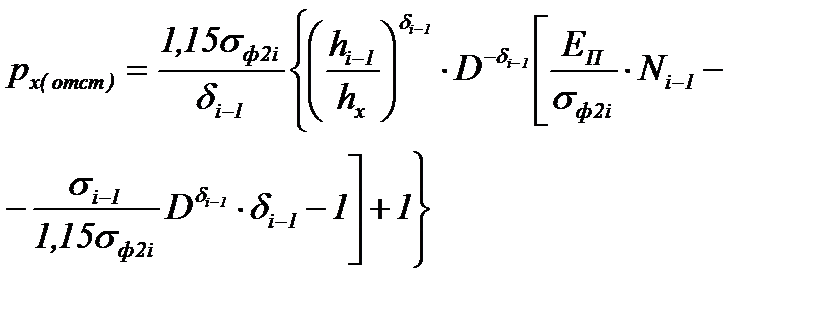
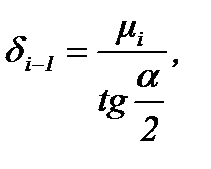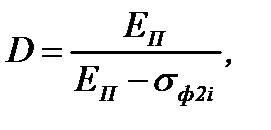
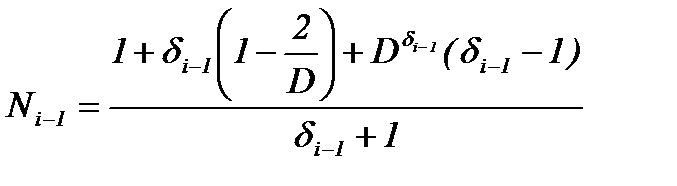
Пластичес-кий – зона опережения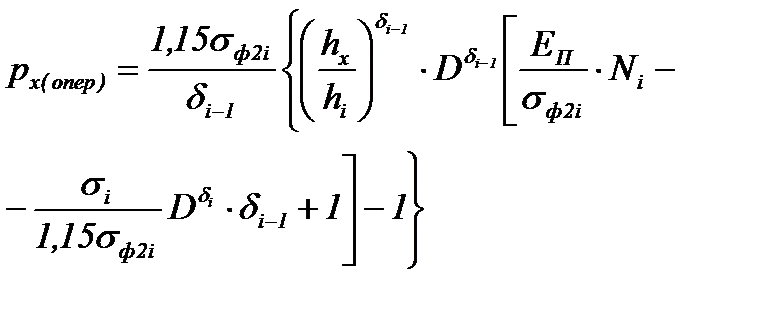

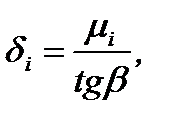
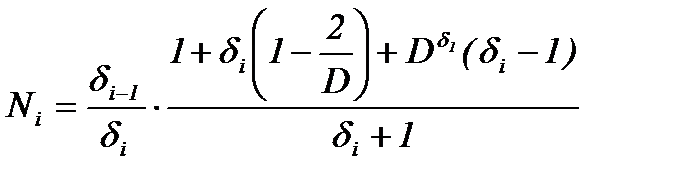
3. Значительное влияние на контактные напряжения оказывает коэффициент трения в очаге деформации μ_i (он входит в формулы p_x(h_x) в связанном виде - через коэффициенты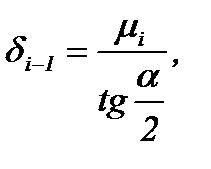

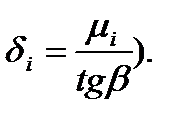
Зависимость p_x(h_x) от μ_i может быть выявлена путем расчетов по формулам таблицы 6.3. Предварительный анализ дает основание утверждать, что эта зависимость носит сложный, нелинейный характер, но решающее влияние на величину p_x(h_x) оказывают члены 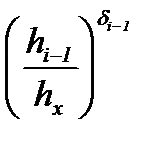, 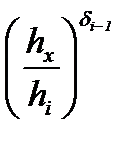в формулах p_x(h_x) пластического участка, которые при увеличении μ_i вызывают существенный рост контактных напряжений.

4. Увеличение заднего и переднего удельных натяжений σ_i-1 и σ_i (они входят в формулы p_x(h_x) пластического участка непосредственно, а на упругих участках – через коэффициенты C_i-1 и C_i) вызывает снижение контактных напряжений.