З) Расчет контактных напряжений в очаге деформации с двумя нейтральными сечениями

Возможность появления такого структурного варианта очага деформации при холодной прокатке обоснована в п. 5.1 главы 5. Если скорость полосы v_x изменяется по длине очага по графику 2 (рис. 5.1), то первое нейтральное сечение N₁N₁ толщиной h_н1 возникает вблизи сечения, где толщина полосы h_x=h_min. В этом случае на втором упругом участке BC скорость полосы v_x, уменьшаясь из-за роста ее толщины h_x, вновь может оказаться меньше окружной скорости бочки валков v_в. Точка N₂ пересечения графиков v_x и v_в определяет положение второго нейтрального сечения N₂N₂, имеющего толщину h_н2.

В результате второй упругий участок BC оказывается разделенным на две зоны: зону опережения BN₂, являющуюся продолжением зоны опережения N₁B пластического участка, и дополнительную зону отставания N₂C, примыкающую к выходному сечению полосы CC.

Структурная схема такого очага деформации в i-й рабочей клети n-клетевого стана и график изменения по длине очага скорости полосы показаны на рис. 6.10.

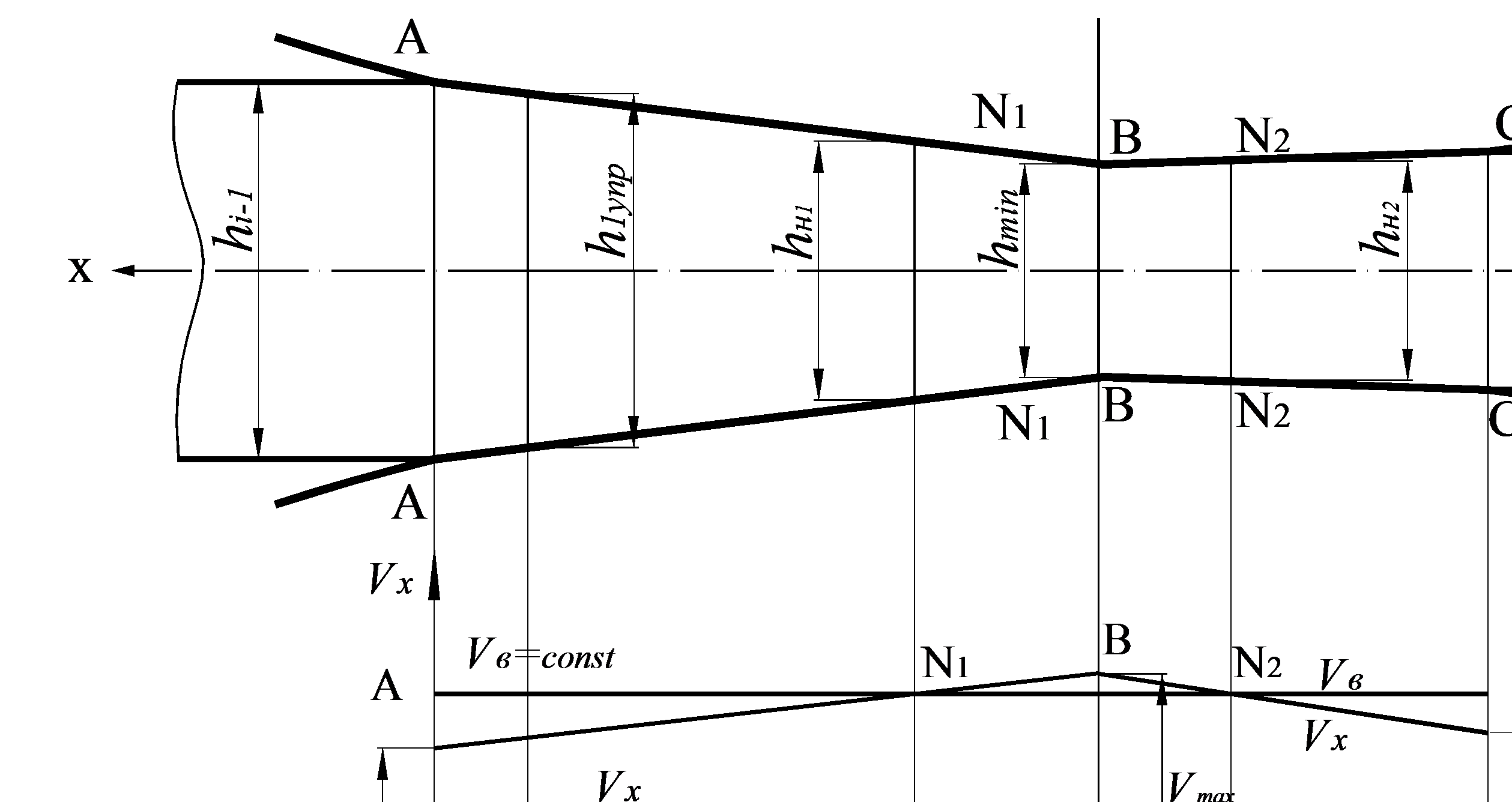
Рис. 6.10 Схема очага деформации с двумя нейтральными сечениями и график изменения скорости полосы по его длине.

Чтобы установить в процессе энергосилового расчета n-клетевого стана, имеется ли в очаге деформации i-ой рабочей клети два нейтральных сечения, следует сравнить между собой три значения толщины полосы:

- толщину в нейтральном сечении h_н, рассчитанную по формуле (6.39);

- минимальную толщину h_min, рассчитанную по формуле (6.49);

- заданную толщину на выходе из валков h_i.

Если оказалось, что h_н< h_min,то в очаге деформации нет ни одного нейтрального сечения (см. п. “ж” данной главы).

Если оказалось, что h_н > h_min, то в очаге деформации есть, по крайней мере, одно нейтральное сечение. В этом случае сравнивают между собой толщины h_н и h_i.

Если оказалось, что h_н > h_i, то данное нейтральное сечение является в очаге деформации единственным, т.к. оно достаточно далеко расположено от сечения с толщиной h_min, и скорость полосы v_x, уменьшаясь на втором упругом участке, остается больше, чем окружная скорость бочки валков.

Расчет контактных напряжений в таком очаге изложен в п. “е” данной главы.

Если же оказалось справедливым неравенство:

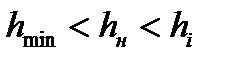, (6.54)

то в очаге деформации есть второе нейтральное сечение. Смысл этого неравенства состоит в том, что первое нейтральное сечение N₁N₁ находится весьма близко к сечению с минимальной толщиной полосы, поэтому, согласно схеме на рис. 6.10:

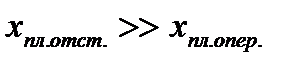
В результате скорость полосы v_x на участке N₁B длиной x_{пл.опер.} увеличивается до значения v_max незначительно и, снижаясь на участке BC, становится в конце этого участка меньше скорости бочки валка: v_i<v_в, т.е. на длине этого участка обязательно будет сечение N₂N₂, в котором v_x<v_в.

Таким образом, неравенство (6.54) является идентификационным признаком очага деформации с двумя нейтральными сечениями. В работе [25], показано, что с погрешностью менее 1% справедливо равенство:

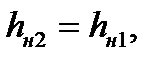, (6.55)

т.е. формулу (6.39) можно использовать для расчета толщины полосы не только в первом, но и во втором нейтральных сечениях.

Следует отметить, что очаги деформации с двумя нейтральными сечениями на практике встречаются не очень часто. Например, в работе [25] приводятся следующие данные. На 5-тиклетевом стане “1700” , оснащенном автоматизированной системой управления технологическим процессом (АСУТП), были проанализированы параметры 131 режима холодной прокатки, охватывающие весь диапазон толщин, ширин и марок сталей. В результате анализа выявлено 17 режимов (13% от общего числа), в которых имеются очаги деформации с двумя нейтральными сечениями, из них 15 очагов в 5-й клети и 2 в 4-й клети. При этом учет 2-го нейтрального сечения позволил уменьшить среднюю погрешность энергосилового расчета с 5,4% до 3,0% (в 1,8 раза), а максимальную погрешность – с 89% до 14% (в 6,5 раз).

После того, как установлено, что очаг деформации i-й рабочей клети содержит 2 нейтральных сечения, можно перейти к расчету контактных напряжений p_x(h_x) в каждом из пяти его участков, показанных на схеме рис. 6.10.

При этом частично можно воспользоваться формулами p_x(h_x), полученными ранее для очагов двух других структурных типов. Так, на первом упругом участке и в зоне отставания пластического участка напряженное состояние полосы такое же, как в очаге деформации с одним нейтральным сечением, поэтому для расчета контактных напряжений на этих участках пригодны формулы p_x(упр) и p_x(отст) таблицы 6.3.

На пятом участке очага деформации с двумя нейтральными сечениями, где находится вторая зона отставания длиной x_{2упр.отст} (рис. 6.10) напряженное состояние полосы такое же, как на втором упругом участке очага деформации без нейтральных сечений. Поэтому для расчета на этом участке контактных напряжений p_x(h_x)= p_{x(2упр.отст)} пригодна формула (6.53).

Формулы p_x(h_x)_(опер) и p_x(h_x)_{(2упр.опер)}, для расчета контактных напряжений в зонах опережения пластического и второго упругого участков ранее отсутствовали. Вывод этих формул производится по той же методике, что и для очагов деформации двух других структурных типов: на каждом участке решают систему трёх уравнений: уравнения (6.21), связывающего напряжения τ_x и p_x через закон трения; уравнения пластичности (6.25) – для зоны опережения пластического участка, или уравнения упругости (6.24) – для зоны опережения второго упругого участка, и дифференциального уравнения равновесия полосы.

Мы рекомендуем изучающим теорию прокатки для более глубокого понимания материала вывести эти формулы самостоятельно, используя методику, изложенную выше, в п.п. “д”,“е”,“ж”. Окончательные выражения p_x(h_x) имеют вид:

- в зоне опережения пластического участка (на участке N₁B, рис. 6.10):

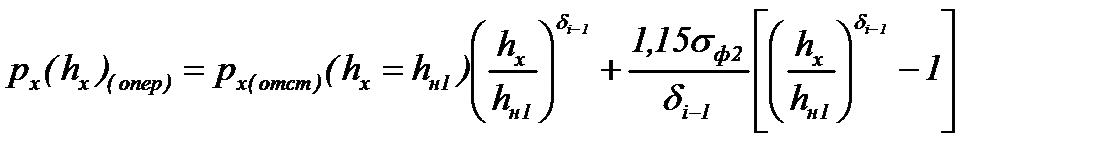; (6.56)

где 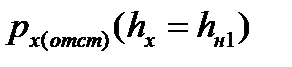- значение напряжения p_x(h_x) в зоне отставания пластического участка, вычисленное по формуле таблицы 6.3. при толщине полосы 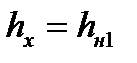(на границе зон отставания и опережения пластического участка).

- в зоне опережения второго упругого участка (на участке BN₂, рис. 6.10):

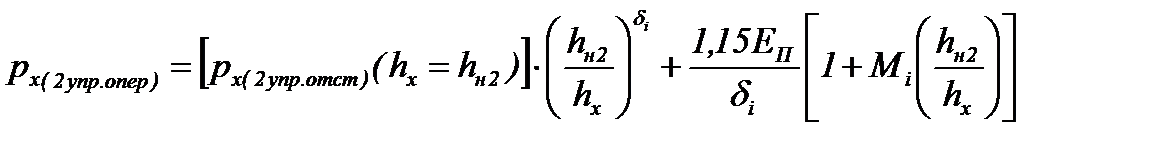; (6.57)

где 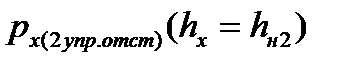- значение напряжения p_x(h_x) в зоне отставания второго упругого участка, вычисленное по формуле (6.53) при толщине полосы 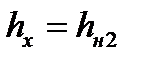(на границе зон опережения и отставания этого участка);

.

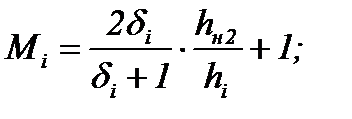
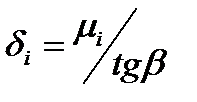Для полной характеристики очага деформации с двумя нейтральными сечениями в таблице 6.4 приведены расчетные формулы его структурных параметров, которые не требовались для расчета очагов других типов. В частности, из-за разделения второго упругого участка на две зоны необходимо вычислить длину каждой из них. Кроме того, из-за изменения формулы p_x(h_x) для зоны опережения пластического участка изменяется её длина, а, следовательно, и длина зоны отставания пластического участка. Формулы расчета остальных структурных параметров – общие для очагов деформации всех типов (см. п. “е” данного параграфа).

Таблица 6.4

Формулы для расчета структурных параметров очага деформации с двумя нейтральными сечениями (см. схему рис. 6.10)

Наименование параметра	Обозначение	Формула	Примечание
Длина зоны опережения пластического участка	Xпл.опер		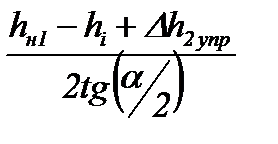hн1 – ф-ла (6.39) Δh2упр – ф-ла (6.15) tg(α/2) – ф-ла (6.50)
Длина зоны отставания пластического участка	Xпл.отст	Xпл - Xпл.опер	Xпл – ф-ла (6.45)
Длина зоны отставания второго упругого участка	X2упр.отст		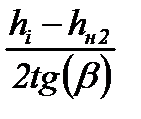hн2 – ф-лы (6.55) и (6.39) tg β – ф-ла (6.51)
Длина зоны опережения второго упругого участка	X2упр.опер	X2упр - X2упр.отст	X2упр – ф-лы (6.40) и (6.41)