Ж) Расчет контактных напряжений в очаге деформации, не имеющем нейтральных сечений

Обоснование возможности появления в процессе холодной прокатке очага деформации, в котором отсутствует нейтральное сечение, изложено в параграфе 5.1 главы 5. На рис. 5.1 этого параграфа показаны три возможных графика изменения скорости полосы v_x по длине очага деформации. Если скорость v_x изменяется по графику 3, она все время остается меньше окружной скорости бочки валков, т.е. весь очаг деформации в этом случае представляет собой зону отставания, а нейтральное сечение в нем отсутствует.

Методика расчета контактных напряжений в таком очаге деформации имеет некоторые отличия от методики, изложенной в п. “е” для очага с одним нейтральным сечением.

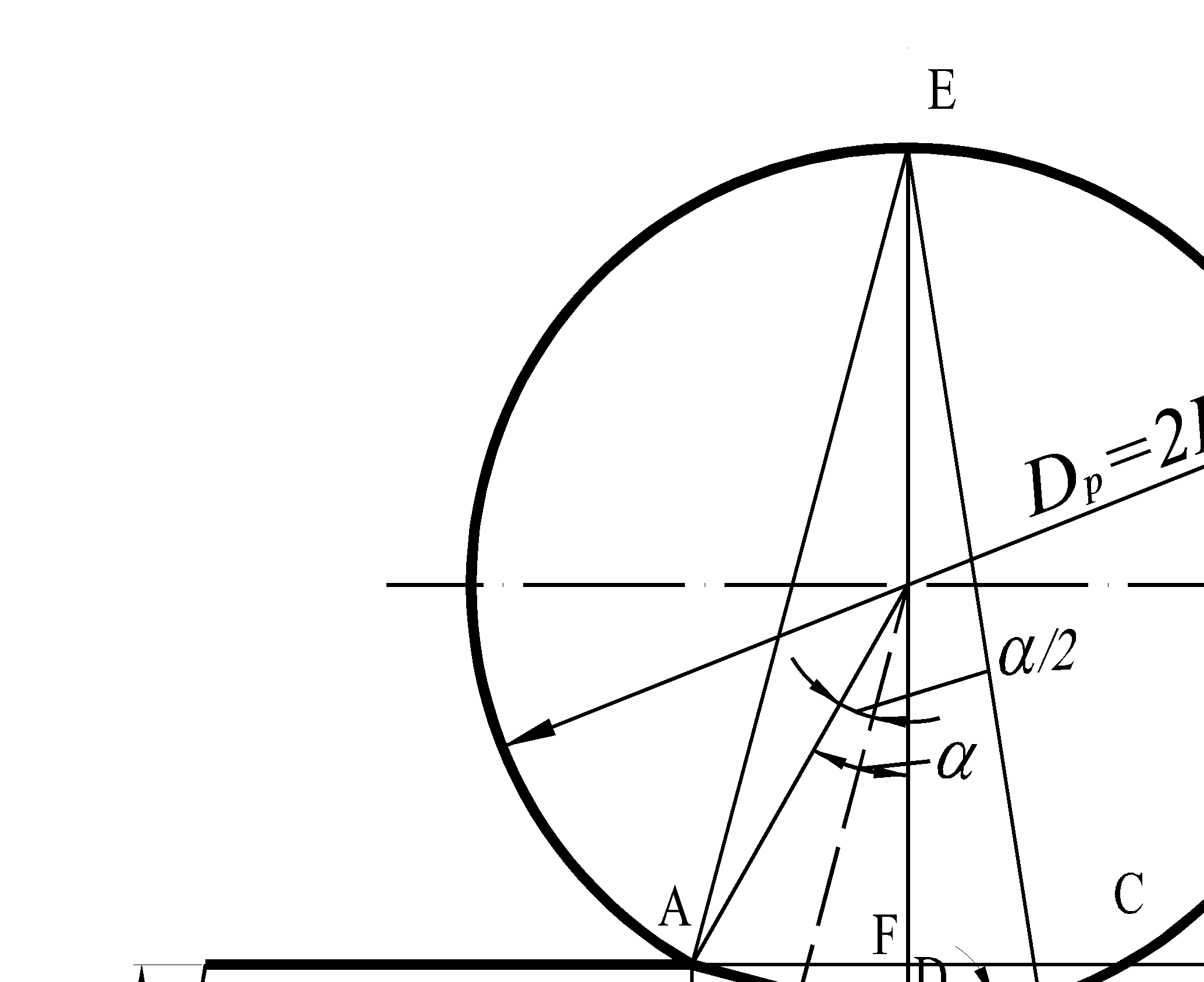
Рис. 6.8 Расчетная схема для определения структурных параметров очага деформации при прокатке тонкой широкой полосы

Следует заметить, что, приступая к энергосиловому расчету процесса прокатки, исполнитель расчета имеет в качестве исходных данных параметры режима прокатки (обжатия, скорости, натяжения) и заранее не знает, какой структурный тип очага деформации имеет место в той или иной рабочей клети.

Поэтому расчет контактных напряжений начинают с предположения, что в очаге деформации имеется нейтральное сечение, и выполняют его по методике, изложенной в п. “е”.

Рассчитав по формулам таблицы 6.3 напряжения p_x(h_x) во всех четырех участках очага деформации, а затем – по формуле (6.39) – толщину полосы в нейтральном сечении, приступают к процедуре идентификации структурного типа очага деформации.

Для этого сравнивают величину h_н, рассчитанную по формуле (6.39), с толщиной h_min, рассчитанной по формуле (6.49).

Если оказалось, что h_н>h_min, это означает, что в очаге деформации есть, по крайней мере, одно нейтральное сечение, т.к. точка пересечения кривых p_x(h_x) для зон отставания и опережения пластического участка очага деформации находится в пределах границ этого участка.

Если оказалось, что h_н<h_min, это означает, что точка пересечения указанных кривых p_x(h_x) находится за пределами очага деформации, т.к. в очаге деформации нет ни одного сечения, в котором h_x<h_min.

Таким образом, условие, позволяющее установить, что очаг деформации не имеет нейтрального сечения (всю его длину занимает зона отставания), имеет вид:

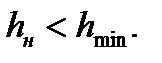(6.52)

В очаге деформации без нейтральных сечений формула p_x(h_x) для первого упругого участка, приведенная в табл. 6.3, остается без изменений: p_x(h_x)=p_x(1упр).

Формула p_x(h_x) для зоны отставания пластического участка, приведенная в табл. 6.3, распространяется в таком очаге деформации на всю длину пластического участка:

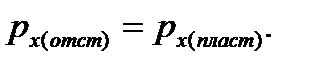
Изменяется лишь формула p_x(h_x) для второго упругого участка очага деформации, т.к. направление касательных напряжений τ_x на этом участке изменилось на противоположное, и, следовательно, изменилось дифференциальное уравнение равновесия элемента полосы, находящегося на втором упругом участке (см. рис. 6.9).

Определение проекций на ось “x” сил, действующих на элемент abdc, находящийся на втором упругом участке очага деформации без нейтрального сечения, было приведено ранее в таблице 6.2.

Уравнение равновесия элемента полосы в этом случае имеет вид:

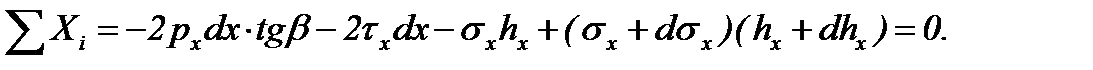
Упростив его, получим:

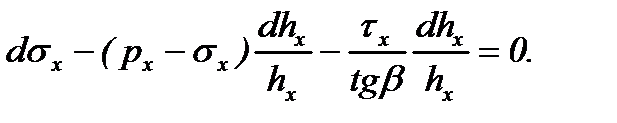
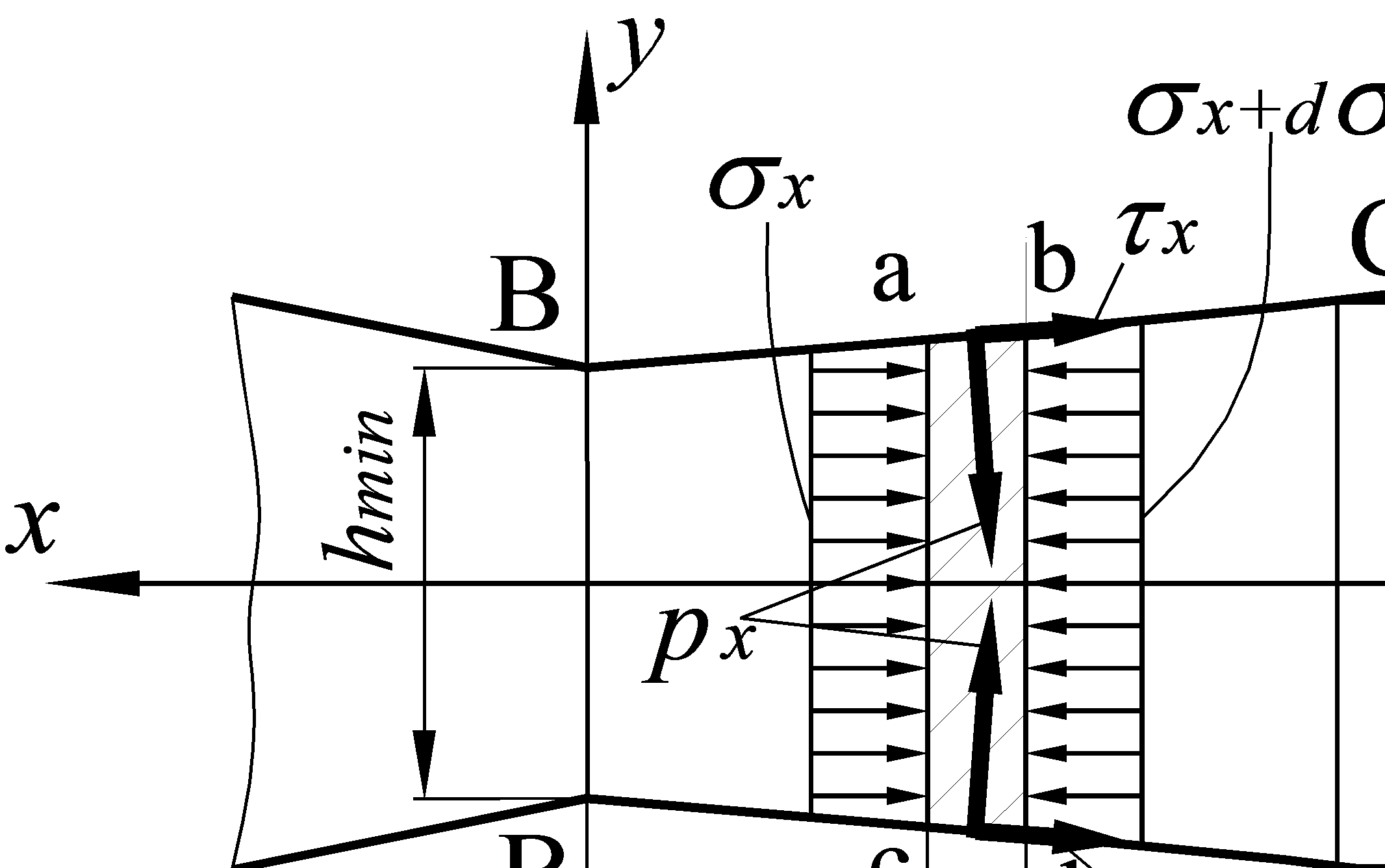
Рис. 6.9 Схема напряжений, действующих на полосу на втором упругом участке, если он находится в зоне отставания.

Последовательность дальнейших преобразований и решения этого уравнения аналогична описанной выше, в п. “д” данной главы (изучающим теорию прокатки рекомендуется проделать все преобразования самостоятельно).

Окончательная расчетная формула p_x(h_x) для второго упругого участка, расположенного в зоне отставания, имеет вид:

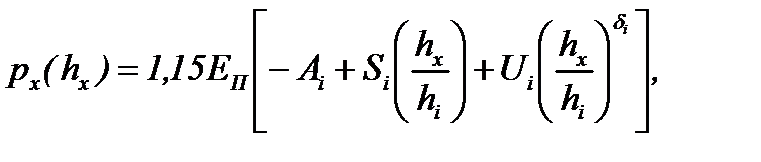(6.53)

где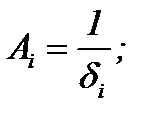

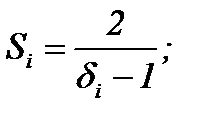
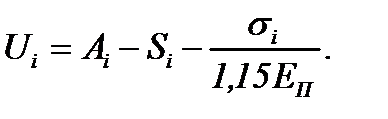
Из формулы (6.53) видно, что закономерности, установленные для очага деформации с одним нейтральным сечением, имеют место и в очаге деформации без нейтральных сечений: напряжения p_x(h_x) на втором упругом участке пропорциональны модулю упругости материала полосы, находятся в сложной зависимости от коэффициента трения и уменьшаются с ростом переднего натяжения.