Г) Система уравнений для получения расчетных формул контактных напряжений
Согласно исходным положениям, изложенным в п. 6.1, и допущениям, сформулированным в подпункте “a” п. 6.3, чтобы получить расчетные формулы контактных напряжений, зависящих от переменной толщины полосы (px(hx), τx(hx), σx(hx)), для каждого участка очага деформации составляют систему из трех уравнений:
первое: дифференциальное уравнение равновесия элемента полосы (см. схему на рис. 6.2,а);
второе: уравнение, выражающее связь касательных напряжений с нормальными, по закону трения скольжения;
третье: уравнение пластичности (на пластических участках) или упругости (на упругих участках).
Так как на всей протяженности очага деформации при холодной прокатке действует закон трения скольжения, в качестве второго уравнения на всех участках (и упругих, и пластическом) может быть принято выражение:
τx=μ px. (6.21)
В качестве третьего уравнения на первом упругом участке очага деформации может быть принято выражение (6.7), которое применительно к i-й клети будет иметь вид:
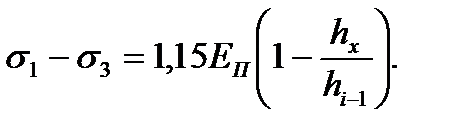 (6.22)
(6.22)
В качестве главных нормальных напряжений σ1, σ3 по рекомендации А.И. Целикова [1;2] можно приближенно принять: σ1 = - σx; σ3 = - px.
Эта рекомендация является обоснованной, т.к. в теории напряжений сжимающие напряжения считаются отрицательными (что объясняет знаки “минус” при напряжениях σx и px), а максимальным из сжимающих главных напряжений считается не самое большое по модулю, а, наоборот, - самое маленькое, т.к. оно ближе остальных к оси растягивающих напряжений.
Прокатка тонких широких полос происходит, как правило, с натяжением; возникающие из-за натяжений растягивающие напряжения в полосе уменьшают величину сжимающих напряжений σx, по сравнению с сжимающими напряжениями σz, направленными поперек движения полосы.
Поэтому вполне логично принять, что σ1= -σx; σ2 = -σz, а самое большое по величине из сжимающих напряжений, которое и обеспечивает пластическую деформацию, играет роль минимального главного нормального напряжения: σ3 = - px.
Подставив указанные значения σ1 и σ3 в уравнение (6.22), для первого упругого участка окончательно получим:
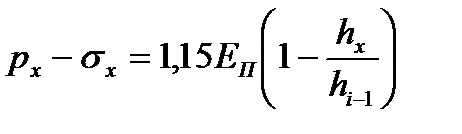 (6.23)
(6.23)
(в выражение (.23), подставляются модули (абсолютные величины) px и σx).
Аналогичное третье уравнение системы для расчета контактных напряжений на втором упругом участке будет иметь вид:
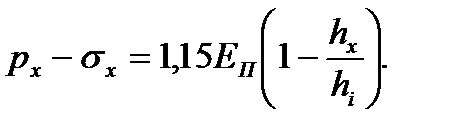 (6.24)
(6.24)
На пластическом участке очага деформации в качестве третьего уравнения используется условие пластичности (6.2), которое для i-й клети непрерывного стана принимает вид:
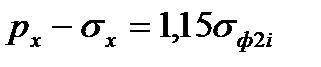 (6.25)
(6.25)
где σф2i – среднее значение условного предела текучести полосы на пластическом участке, определяемое по формуле (6.19).
Чтобы составить первое уравнение системы, необходимой для расчета контактных напряжений – дифференциальное уравнение равновесия полосы - на каждом участке очага деформации, согласно схеме рис. 6.2,а на расстоянии “x” от начала координат выделяют элемент abdc, имеющий размеры: длину по оси прокатки dx, высоту в сечении bd: hx, высоту в сечении ac: hx+dhx. Углы наклона дуг “ab” и “bc” на первом упругом и пластическом участках равны α/2, на втором упругом участке равны β.
Уравнение равновесия элемента abdc принимают в виде:
ΣXj = 0, (6.26)
где Xj – проекции сил, действующих, по наружным граням на выделенный элемент. Эти силы вызваны напряжениями на площадках контакта с валками ab, cd и в вертикальных сечениях bd, ac.
Чтобы перейти от напряжений к проекциям сил, надо определить площади всех этих граней, умножить каждое напряжение на площадь соответствующей грани, получив величину силы, а затем вычислить ее проекцию на ось прокатки “x”.
Результаты этих операций показаны в таблице 6.2. Необходимо обратить внимание на знаки проекций сил, вызванных касательными напряжениями τx: в зоне отставания они отрицательные, т.к. τx направлены противоположно положительному направлению оси “x” (см. схему на рис. 6.2,а), а в зоне опережения – положительные.
Кроме того, проекции нормальных контактных напряжений px на втором упругом участке отрицательные, а на всех предыдущих участках – положительные. Это объясняется разным направлением углов α/2 и β, характеризующих контур очага деформации.
Таким образом, из трех уравнений системы, составляемой для получения расчетных формул контактных напряжений, только второе выражение (6.21) – одинаковое для всех участков очага деформации.
Из этого следует, что расчетные формулы px(hx), τx(hx), σx(hx) необходимо получать отдельно для каждого участка очага деформации.
Таблица 6.2
Определение проекций на ось “x” сил, действующих на элемент abdc (рис.6.2)
| Грань элемен-та abdc | Участок очага деформации | Площадь грани | Напря-жение | Сила | Проекция силы на ось “x” 3) | |
| ab; cd | первый упругий; зона отставания пластического участка | 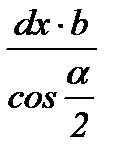
| 1) | 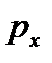
| 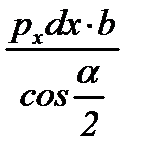
| 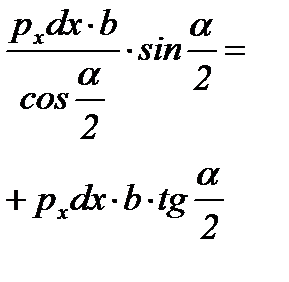
|
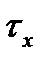
| 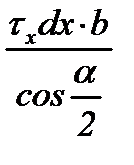
| 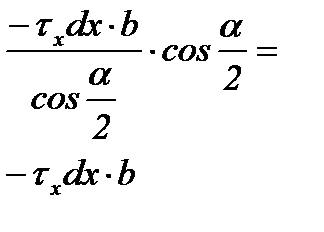
| ||||
| зона опережения пластического участка | 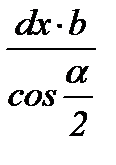
| 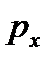
| 
| 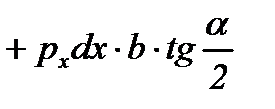
| ||

| 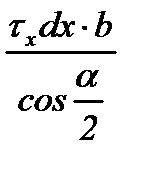
| 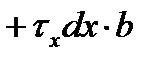
| ||||
| второй упругий, зона опережения | 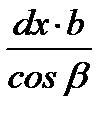
| 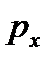
| 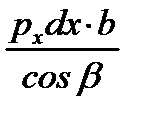
| 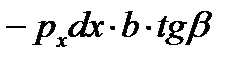
| ||

| 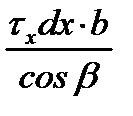
| 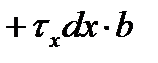
| ||||
| второй упругий, зона отставания2) | 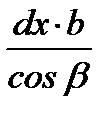
| 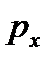
| 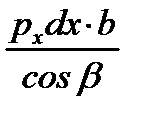
| 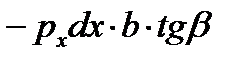
| ||

| 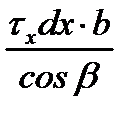
| 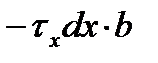
| ||||
| bd | все участки, кроме второго упругого | 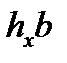
| 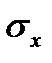
| 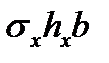
| 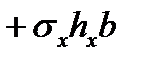
| |
| второй упругий | 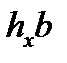
| 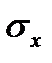
| 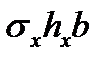
| 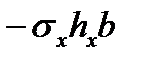
| ||
| ac | все участки, кроме второго упругого | 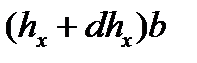
| 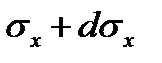
| 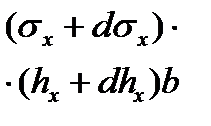
| 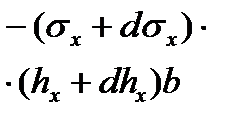
| |
| второй упругий | 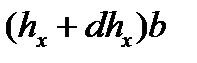
| 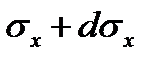
| 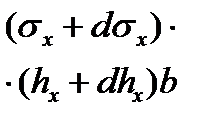
| 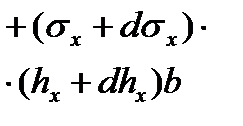
|
Примечания: 1) b – ширина полосы.
2) для очагов без нейтральных сечений и с двумя нейтральными сечениями.
3) положительное направление оси x противоположно направлению движения полосы.
д) Решение системы уравнений – получение расчетных формул px(hx), τx(hx), σx(hx)
Вывод формул px(hx), τx(hx), σx(hx) продемонстрируем на примере решения этой задачи для первого упругого участка очага деформации.
Подставив в уравнение равновесия (6.26) из таблицы 6.2 выражения проекций сил, действующих на гранях ab, cd, bd, ac (рис. 6.2), относящиеся к первому упругому участку, получим:
+2 px dx tg(α/2) - 2 τx dx + σx hx - (σx+dσx)(hx+dhx) = 0. (6.27)
Входящий во все члены уравнения (6.27) множитель “b” (ширина полосы) сокращен, т.е. от ширины полосы контактные напряжения при холодной прокатке тонких полос не зависят.
Чтобы упростить уравнение (6.27), выразим отрезок dx через приращение толщины dhx. Для этого рассмотрим в увеличенном масштабе верхнюю часть элемента abdc (см. рис. 6.7).
Из рис. 6.7 получим:
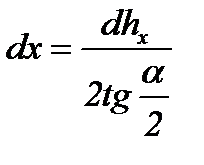 (6.28)
(6.28)

Рис. 6.7. Верхняя часть элемента abdc на рис. 6.2. в
увеличенном масштабе
Подставив это выражение dx в уравнение (6.27) и выполнив несложные преобразования, получим:
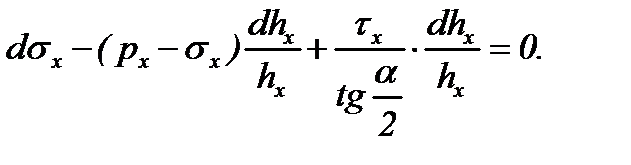 (6.29)
(6.29)
Дата добавления: 2019-02-08; просмотров: 1283;











