Модели кровообращения

Рассмотрим гидродинамическую модель кровеносной системы, предложенную О. Франком. Несмотря на достаточную простоту, она позволяет установить связь между ударным объемом крови артерии) поступает кровь из сердца, объ­емная скорость кровотока равна Q. От упругого резервуара кровь оттекает с объемной скоростью кровотока Q_o в п(объем крови, выбрасываемый желу­дочком сердца за одну систолу), гид­равлическим сопротивлением перифе­рической части системы кровообраще­ния Х_о и изменением давления в артериях. Артериальная часть систе­мы кровообращения моделируется упругим (эластичным) резервуаром (рис. 9.1, обозначено УР). Так как кровь находится в упругом резервуаре, то ее объем V в любой момент времени зависит от давления ρ по следующему соотношению:

где κ— эластичность, упругость резервуара (коэффициент про­порциональности между давлением и объемом), V₀ — объем ре­зервуара при отсутствии давления (ρ = 0). Продифференцировав (9.1), получим

В упругий резервуар (артерии) поступает кровь из сердца, объемна скорость кровотока равна Q. Предполагаем, что гидравлическое сопротивление периферической системы постоянно. Это мо­делируется «жесткой» трубкой на выходе упругого резервуара (рис. 9.1).

Можно составить достаточно очевидное уравнение (рис. 9.1)

показывающее, что объемная скорость кровотока из сердца равна сумме скорости возрастания объема упругого резервуара и скорос­ти оттока крови из упругого резервуара.

На основании уравнения Пуазейля (7.8) и формулы (7.9) мож­но записать для периферической части системы

где р — давление в упругом резервуаре, р_в — венозное давление, оно может быть принято равным нулю, тогда вместо (9.4) имеем

Q₀=ρ/X₀ (9.5)

Подставляя (9.2) и (9.5) в (9.3), получаем

Проинтегрируем (9.6). Пределы интегрирования по времени соот­ветствуют периоду пульса (периоду сокращения сердца) от 0 до Т_п. Этим временным пределам соответствуют одинаковые давления — минимальное диастолическое давление р_д :

Интеграл с равными пределами равен нулю, поэтому из (9.7) имеем

Экспериментальная кривая, показывающая временную зависи­мость давления в сонной артерии, приведена на рис. 9.2 (сплошная линия). На рисунке показан период пульса, длительности Т_с сис­толы и Т_д диастолы, р_с — максимальное (систолическое) давление.

Интеграл в левой части уравнения (9.8) равен объему крови, который выталкивается из сердца за одно сокращение, — удар­ный объем. Он может быть найден экспериментально. Интеграл в правой части уравнения (9.8) соответствует площади фигуры, ог­раниченной кривой и осью времени (см. рис. 9.2), что также мож­но найти. Используя указанные значения интегралов, можно вы­числить по (9.8) гидравлическое сопротивление периферической части системы кровообращения.

Во время систолы (сокращение серд­ца) происходит расширение упругого резервуара, после систолы, во время ди­астолы — отток крови к периферии, Q = 0. Для этого периода из (9.6) имеем

Соответствующая кривая изображена тонкой линией на рис. 9.2. На основании (9.5) получаем зависимость объемной скорости оттока крови от времени:

где Q_c= P_с/X₀ объемная скорость кровотока из упругого резервуара в конце систолы (начале диастолы).

Зависимости (9.10) и (9.11) представляют собой экспоненты. Хотя данная модель весьма грубо описывает реальное явление, она чрезвычайно проста и верно отражает процесс к концу диасто­лы. Вместе с тем изменения давления в начале диастолы с по­мощью этой модели не описываются.

На основе механической модели по аналогии может быть по­строена электрическая модель (рис. 9.3).

Здесь источник U, дающий несинусоидальное переменное элект­рическое напряжение, служит аналогом сердца, выпрямитель В — сердечного клапана. Конденсатор С в течение полупериода накап­ливает заряд, а затем разряжается на резистор R, таким образом происходит сглаживание силы тока, протекающего через резистор. Действие конденсатора аналогично действию упругого резервуара (аорты, артерии), который сглаживает колебание давления крови в артериолах и капиллярах. Резистор является электрическим аналогом периферической сосудистой системы.

В более точной модели сосудистого русла использовалось боль­шее количество эластичных резервуаров для учета того факта, что сосудистое русло является системой, распределенной в простран­стве. Для учета инерционных свойств крови при построении моде­ли предполагалось, что эластичные резервуары, моделирующие восходящую и нисходящую ветви аорты, обладают различной уп­ругостью. На рис. 9.4 приведено изображение модели Ростона, со­стоящей из двух резервуаров с различными эластичностями (упругостями) и с неупругими звеньями разного гидравлического со-

противления между резервуарами. Этой модели соответствует электрическая схема, изображенная на рис. 9.5. Здесь источник тока задает пульси­рующее напряжение U(t), являющее­ся аналогом давления p(t); емкости С₁ и С₂ соответствуют упругостям резер­вуаров k_l и k₂, электрические сопро­тивления R_1, R₂ и R₃ — гидравличе­ским сопротивлениям X_1, Х₂ и Х₃, си-

лы тока 1₁ и 1₂ — объемным скоростям оттока крови Q₁ и Q₂.

Такая модель математически описывается системой двух диф­ференциальных уравнений первого порядка, их решение дает две кривые, соответствующие первой и второй камерам.

Двухкамерная модель лучше описывает процессы, происходя­щие в сосудистом русле, но и она не объясняет колебания давле­ния в начале диастолы.

Модели, содержащие несколько сотен элементов, называют мо­делями с распределенными параметрами.

Пульсовая волна

При сокращении сердечной мышцы (систола) кровь выбрасыва­ется из сердца в аорту и отходящие от нее артерии. Если бы стенки этих сосудов были жесткими, то давление, возникающее в крови на выходе из сердца, со скоростью звука передалось бы к перифе­рии. Упругость стенок сосудов приводит к тому, что во время сис­толы кровь, выталкиваемая сердцем, растягивает аорту, артерии и артериолы, т. е. крупные сосуды воспринимают за время систолы больше крови, чем ее оттекает к периферии. Систолическое давле­ние человека в норме равно приблизительно 16 кПа. Во время рас­слабления сердца (диастола) растянутые кровеносные сосуды спа­дают и потенциальная энергия, сообщенная им сердцем через кровь, переходит в кинетическую энергию тока крови, при этом поддерживается диастолическое давление, приблизительно равное 11 кПа.

Распространяющуюся по аорте и артериям волну повышенного давления, вызванную выбросом крови из левого желудочка в пе­риод систолы, называют пульсовой волной.

Пульсовая волна распространяется со скоростью 5—10 м/с и даже более. Следовательно, за время систолы (около 0,3 с) она

должна распространиться на расстоя­ние 1,5—3 м, что больше расстояния от сердца к конечностям. Это означает, что начало пульсовой волны достигнет конечностей раньше, чем начнется спад давления в аорте. Профиль части арте­рии схематически показан на рис. 9.6: а — после прохождения пульсовой вол­ны, б — в артерии начало пульсовой волны, в — в артерии пульсовая волна, г — начинается спад повышенного дав­ления.

Д1ульсовой волне будет соответство­вать пульсирование скорости кровото­ка в крупных артериях, однако ско­рость крови (максимальное значение

0,3—0,5 м/с) существенно меньше скорости распространения пульсовой волны.

Из модельного опыта и из общих представлений о работе серд­ца ясно, что пульсовая волна не является синусоидальной (гармо­нической). Как всякий периодический процесс, пульсовая волна может быть представлена суммой гармонических волн (см. § 5.4). Поэтому уделим внимание, как некоторой модели, гармониче­ской пульсовой волне.

Предположим, что гармоническая волна [см. (5.48)] распрост­раняется по сосуду вдоль оси X со скоростью v. Вязкость крови и упруговязкие свойства стенок сосуда уменьшают амплитуду вол­ны. Можно считать (см., например, § 5.1), что затухание волны будет экспоненциальным. На основании этого можно записать следующее уравнение для пульсовой волны:

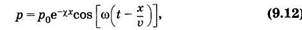
где р₀ — амплитуда давления в пульсовой волне; х — расстояние до произвольной точки от источника колебаний (сердца); t — вре­мя; ω — круговая частота колебаний; χ — некоторая константа, определяющая затухание волны. Длину пульсовой волны можно найти из формулы

Волна давления представляет некоторое «избыточное» давле­ние. Поэтому с учетом «основного» давления р_а (атмосферное давление или давление в среде, окружающей сосуд) можно измене­ние Явления записать следующим образом:

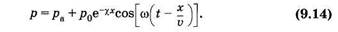
Как видно из (9.14), по мере продвижения крови (по мере уве­личения х) колебания давления сглаживаются. Схематично на рис. 9.7 показано колебание давления в аорте вблизи сердца (а) и в артериолах (б). Графики даны в предположении модели гармо­нической пульсовой волны.

На рис. 9.8 приведены экспериментальные графики, показы­вающие изменение среднего значения давления и скорости v_кр кровотока в зависимости от типа кровеносных сосудов. Гидроста­тическое давление крови не учитывается. Давление — избыточ­ное над атмосферным. Заштрихованная область соответствует ко­лебанию давления (пульсовая волна).

Скорость пульсовой волны в крупных сосудах следующим об­разом зависит от их параметров (формула Моенса—Кортевега):

где Е — модуль упругости, р — плотность вещества сосуда, h — толщина стенки сосуда, d — диаметр сосуда.

Интересно сопоставить (9.15) с выражением для скорости рас­пространения звука в тонком стержне

У человека с возрастом модуль упругости сосудов возрастает, поэтому, как следует из (9.15), становится больше и скорость пульсовой волны.