Определение скорости кровотока

Существует несколько методов определения скорости кровото­ка. Рассмотрим физические основы двух из них.

Ультразвуковой метод (ультразвуковая расходеметрия) основан на эффекте Доплера (см. § 5.10). От генератора I электри­ческих колебаний УЗ-частоты (рис. 9.15) сигнал поступает на из­лучатель 2 и на устройство сравнения частот 3. УЗ-волна 4 прони­кает в кровеносный сосуд 5 и отражается от движущихся эритро­цитов 6. Отраженная УЗ-волна 7 попадает в приемник 8, где преобразуется в электрическое колебание и усиливается. Усилен­ное электрическое колебание попадает в устройство 3. Здесь срав­ниваются колебания, соответствующие падающей и отраженной волнам, и выделяется доплеровский сдвиг частоты в виде электрического колебания:

Из формулы (5.65) можно определить скорость эритроцитов:

В крупных сосудах скорость эритроцитов различна в зависи­мости от их расположения относительно оси: «приосевые» эрит­роциты движутся с большей скоростью, а «пристеночные» — с меньшей. УЗ-волна может отражаться от разных эритроцитов, поэтому доплеровский сдвиг получается не в виде одной частоты, а как интервал частот. Таким образом, эффект Доплера позволяет определять не только среднюю скорость кровотока, но и скорость движения различных слоев крови.

Электромагнитный метод (электромагнитная расходометрия) измерения скорости кровотока основан на отклонении движущихся зарядов в магнитном поле. Дело в том, что кровь, бу­дучи электрически нейтральной системой, состоит из положи­тельных и отрицательных ионов. Следовательно, движущаяся кровь является потоком заряженных частиц, которые перемещаются со скоростью У_кр. На движущийся электрический заряд q в магнитном поле с индукцией В действует сила (см. § 13.3)

Если заряд отрицательный, то сила направлена противоположно векторному произведению v_крх В.

Как показано на рис. 9.16, силы, действующие со стороны маг­нитного поля на разноименные заряды, направлены в противоположные стороны. Около одной стенки кровеносного сосуда преоб­ладает положительный заряд, около другой — отрицательный.
Перераспределение зарядов по сечению сосуда вызовет появление электрического поля.

Возникающее электрическое напряжение U (см. рис. 9.16) зависит от ско­рости движения ионов, т. е. от скорости крови [см. (9.19)]. Таким образом, из­меряя это напряжение, можно опреде­лить и скорость кровотока. Зная сече­ние S сосуда, нетрудно вычислить объ­емную скорость кровотока (м³/с):

Практически удобнее в этом методе использовать переменное магнитное поле (рис. 9.17). Это приводит к возникновению переменного напряжения U, котopoe затем усиливается и измеряется.

Р А З Д Е Л 3

Термодинамика. Физические процессы в биологических мембранах

разделе рассматриваются явления, сущность которых определяется хаотическим движени­ем огромного числа молекул, из которых состоят тела разной при­роды. Изучая эти явления, применяют два основных метода. Один из них — термодинамический, он исходит из основных опытных законов, получивших название начал (законов, принци­пов) термодинамики. При таком подходе не учитывается внутрен­нее строение вещества.

Другой метод — молекулярно-кинетический (статистиче­ский) — основан на представлении о молекулярном строении ве­щества. Учитывая, что число молекул в любом теле очень велико, можно, используя теорию вероятностей, установить определен­ные закономерности.

В разделе в разной степени используются оба подхода.

Медикам данные вопросы важны для понимания энергетики организма, теплообмена биологических систем с окружающей средой, выяснения физических процессов, происходящих в био­логических мембранах, и др.

Г Л А В А 10 Термодинамика

Под термодинамикой понимают раздел физики, рассматри­вающий тела, между которыми возможен обмен энергией (термодинамические системы), без учета микроскопическо­го строения тел, составляющих систему. Различают термоди­намику равновесных систем или систем, переходящих к рав­новесию (классическая, или равновесная, термодинамика, часто называемая просто термодинамикой), и термодинами­ку неравновесных систем (неравновесная термодинамика). Неравновесная термодинамика играет особую роль для рас­смотрения биологических систем.

В главе наряду с термодинамикой изложены также вопросы, связанные с использованием низких температур и нагретых сред для лечения, а также элементы термометрии и калори­метрии.

Основные понятия термодинамики. Первое начало термодинамики

Состояние термодинамической системы характеризуется фи­зическими величинами, называемыми параметрами системы (объем, давление, температура, плотность и т. д.).

Если параметры системы при взаимодействии ее с окружающи­ми телами не изменяются с течением времени, то состояние систе­мы называют стационарным. Примерами таких состояний в те­чение небольшого отрезка времени являются состояние внутрен­ней части работающего домашнего холодильника, состояние тела Человека, состояние воздуха в отапливаемом помещении и т. д.

В разных частях системы, находящейся в стационарном со­стоянии, значения параметров обычно различаются: температура в разных участках тела человека, концентрация диффундирую­щих молекул в разных частях биологической мембраны и т. п. В системе, таким образом, поддерживаются постоянные градиен­ты некоторых параметров, с постоянной скоростью могут проте­кать химические реакции.

Стационарное состояние поддерживается за счет потоков энер­гии и вещества, проходящих через систему. Схематически на рис. 10.1, а показано стационарное состояние, температура неодина­кова в разных точках системы. Ясно, что в стационарном состоя­нии могут находиться такие системы, которые либо обменивают­ся и энергией, и веществом с окружающими системами (откры­тые системы), либо обмениваются только энергией (закрытые системы).

Термодинамическая система, которая не обменивается с окружающими телами ни энергией, ни веществом, называет­ся изолированной. Изолированная система со временем прихо­дит в состояние термодинамического равновесия. В этом состоя­нии, как и в стационарном, параметры системы сохраняются не­изменными во времени. Существенно, что в равновесном состоянии параметры, не зависящие от массы или числа частиц (давление, температура и др.), одинаковы в разных частях этой системы.

Естественно, что любая реальная термодинамическая система не будет изолированной хотя бы потому, что ее невозможно окру­жить оболочкой, не проводящей теплоту. Изолированную систе­му можно рассматривать как удобную термодинамическую мо­дель. Схематически равновесное состояние изолированной систе­мы показано на рис. 10.1, б.

Рассмотрим подробнее взаимодействие закрытой системы с ок­ружающими телами. Обмен энергией между ними может осу­ществляться в двух различных процессах при совершении работы и при теплообмене.

Мерой передачи энергии в процессе теплообмена является количество теплоты, а мерой передачи энергии в процессе соверше­ния работы является работа[1][1][1].

Найдем выражение для вычисле­ния работы, совершаемой газом при изменении его объема. Предположим, что газ, находящийся в цилиндриче­ском сосуде под поршнем, изобарно расширяется от V₁ до V₂ (рис. 10.2), при этом поршень перемещается на расстояние ∆l = l₂ – l₁, а объем изменя­ется на AV = V₂-V₁

На поршень, площадь поперечногосечения которого S, со стороны газа вследствие давления р действует сила F = pS. Так как направле­ние этой силы совпадает с направлением перемещения поршня, то работа, совершаемая газом,

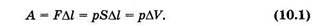
При расширении газа AF > 0 и работа положительна (∆V > 0); при сжатии ∆V < 0 и А < 0. Заметим, что речь идет о работе, совер­шаемой газом, а не внешними силами. Работа всех внешних сил, наоборот, при расширении газа окажется отрицательной, а при сжатии — положительной.

Если при изменении объема давление газа изменяется, то сле­дует вычислять элементарную работу, соответствующую доста­точно малому изменению объема dV:

dA=pdV (10.2)

Проинтегрировав (10.2), получим работу, совершаемую газом:

В качестве примера найдем работу идеального газа при изотер­мическом процессе. Для этого подставим в формулу (10.3) вместо давления его выражение из уравнения Менделеева — Клапейрона:

Получим

Здесь m — масса газа, М — молярная масса (масса моля), Т — термодинамическая температура, Д = 8,31 Дж/(моль • К) — мо­лярная газовая постоянная.

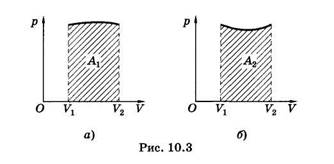
Из уравнения (10.3) ясно, что работа, совершаемая газом, гра­фически определяется как площадь криволинейной трапеции в координатах давление — объем (рис. 10.3). Из рисунка, на кото­ром представлены графики двух различных процессов с одинако­вым начальным и конечным состояниями, видно, что работа зави­сит от процесса. Так, работа А₁ (рис. 10.3, а) больше, чем работа А₂ (рис. 10.3, б).

Закон сохранения энергии для тепловых процессов формули­руется как первое начало термодинамики. Количество тепло­ты, переданное системе, идет на изменение внутренней энер­гии системы и совершение системой работы:

Под внутренней энергией системы понимают сумму кинети­ческой и потенциальной энергий частиц, из которых состоит сис­тема.

Внутренняя энергия U является функцией состояния системы и для данного состояния имеет вполне определенное значение; ∆U есть разность двух значений внутренней энергии, соответствую­щих конечному и начальному состояниям системы: ∆U = U₂ — U₁

Количество теплоты Q, как и работа, является функцией про­цесса, а не состояния. И количество теплоты, и работу нельзя вы­разить в виде разности двух значений какого-либо параметра в конечном и начальном состояниях. В связи с этим Q и А в (10.6) записаны без знака приращения ∆.

Для достаточно малых значений Q, А и малых приращений U используют соответственно обозначения δQ, δА и dU, подчерки­вая этим отличие понятий количества теплоты и работы от внут­ренней энергии.

Ради упрощения в дальнейшем используются одинаковые обо­значения (dQ, dA и dU), однако следует помнить различие этих

физических величин. С учетом изложенного первое начало термо­динамики можно записать в виде:

Значения Q, A, ∆U и dQ, dA, dU могут быть как положительными (теплота передается системе внешними телами, внутренняя энер­гия увеличивается, газ расширяется), так и отрицательными (теплота отнимается от системы, внутренняя энергия уменьшает­ся, газ сжимается).