Механические свойства биологических тканей

Под механическими свойствами биологических тканей пони­мают две их разновидности. Одна связана с процессами биологи­ческой подвижности: сокращение мышц животных, рост клеток, движение хромосом в клетках при их делении и др. Эти процессы обусловлены химическими процессами и энергетически обеспечи­ваются АТФ, их природа рассматривается в курсе биохимии. Ус­ловно указанную группу называют активными механическими свойствами биологических систем. Другая разновидность — пас­сивные механические свойства биологических тел. Рассмотрим этот вопрос применительно к биологическим тканям.

Как технический объект биологическая ткань — композици­онной материал, он образован объемным сочетанием химически разнородных компонентов. Механические свойства биологиче­ской ткани отличаются от механических свойств каждого компо­нента, взятого в отдельности. Методы определения механических свойств биологических тканей аналогичны методам определения этих свойств у технических материалов.

Костная ткань. Кость — основной материал опорно-двига­тельного аппарата. В упрощенном виде можно считать, что ²/₃ мас­сы компактной костной ткани (0,5 объема) составляет неорганиче­ский материал, минеральное вещество кости — гидроксилапатит ЗСа₃(РО₄)₂ • Са(ОН)₂. Это вещество представлено в форме микро­скопических кристалликов. В остальном кость состоит из органи­ческого материала, главным образом коллагена (высокомолеку­лярное соединение, волокнистый белок, обладающий высокоэластичностью). Кристаллики гидроксилапатита расположены между коллагеновыми волокнами (фибриллами).

Плотность костной ткани 2400 кг/м³. Ее механические свойства зависят от многих факторов, в том числе от возраста, индивидуаль­ных условий роста организма и, конечно, от участка организма.

Композиционное строение кости придает ей нужные механиче­ские свойства: твердость, упругость и прочность. Зависимость σ = = f(ε) для компактной костной ткани имеет характерный вид, по­казанный на рис. 8.18, т. е. подобна аналогичной зависимости для твердого тела (см. рис. 8.13); при небольших деформациях выполняется закон Гука. Модуль Юнга около 10 ГПа, предел про­чности 100 МПа. Полезно эти данные сопоставить с данными для капрона, армированного стеклом (см. табл. 16, заметно хорошее соответствие).

Примерный вид кривых ползучести компактной костной тка­ни приведен на рис. 8.19. Участок 0А соответствует быстрой де-

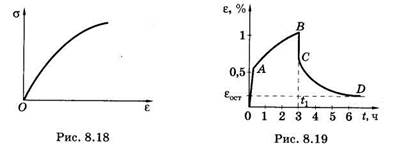
формации, АВ — ползучести. В момент t₁ соответствующий точ­ке В, нагрузка была снята. ВС соответствует быстрой деформации сокращения, CD — обратной ползучести. В результате даже за - длительный период образец кости не восстанавливает своих прежних размеров, сохраняется некоторая остаточная деформация ε_ост.

Этой зависимости приближенно соответствует модель (рис. 8.20, а), сочетающая последовательное соединение пружины с моделью Кельвина—Фойхта. Временная зависимость относительной деформации показана на рис. 8.20, б. При действии постоян- ной нагрузки мгновенно растягивается пружина 1 (участок ОА), затем вытягивается поршень (ползучесть АВ), после прекращения нагрузки происходит быстрое сжатие пружины 1 (ВС), а пружинa 2 втягивает поршень в прежнее положение (ползучесть CD). В предложенной модели не предусматривается остаточная деформация.

Схематично можно заключить, что минеральное содержимое и кости обеспечивает быструю деформацию, а полимерная часть (коллаген) определяет ползучесть.

Если в кости или в ее механической модели быстро создать постоянную деформацию, то скачкообразно возникает и напряжение (участок ОА на рис. 8.20, в). На модели это означает растяжение пру­жины 1 и возникновение в ней напря­жения. Затем (участок АВ) эта пру­жина будет сокращаться, вытягивая поршень и растягивая пружину 2, на пряжение в системе будет убывать r (релаксация напражения). Однако даже спустя значительное время сохра­нится остаточное напряжение σ_ост. Для модели это означает, что не возникнет при постоянной деформации такой ситуации, чтобы пружины вернулись в недеформированное состоя ние.

Кожа. Она состоит из волокон кол­лагена, эластина (так же как и колла­ген, волокнистый белок) и основной ткани — матрицы. Коллаген состав­ляет около 75% сухой массы, а эластин — около 4%. Примерные данные по механическим свойствам приведены в табл. 17.

Эластин растягивается очень сильно (до 200—300%), пример­но как резина. Коллаген может растягиваться до 10%, что соот­ветствует капроновому волокну.

Таблица 17

Из сказанного ясно, что кожа является вязкоупругим материа­лом с высокоэластическими свойствами, она хорошо растягивает­ся и удлиняется.

Мышцы. В состав мышц входит соединительная ткань, со­стоящая из волокон коллагена и эластина. Поэтому механические свойства мышц подобны механическим свойствам полимеров.

Релаксация напряжения в гладких мышцах соответствует модели Максвелла (см. рис. 8.15, в; 8.16, б). Поэтому гладкие мышцы могут значительно растягиваться без особого напряжения, что способствует увеличению объема полых органов, например мочевого пузыря.

Механическое поведение скелетной мышцы соответствует мо­дели, представленной на рис. 8.20, а. При быстром растяжении мышц на определенную величину напряжение резко возрастает, а затем уменьшается до σ_ост (см. рис. 8.20, в).

Зависимость σ = f(ε) для скелетной мышцы нелинейна (рис. 8.21). Анализ этой кривой показывает, что примерно до ε ≈ 0,25 в порт­няжной мышце лягушки механизм деформации обусловлен рас­прямлением молекул коллагена (см. § 8.3). При большей деформа­ции происходит увеличение межатомных расстояний в молекулах.

Ткань кровеносных сосудов (сосудистая ткань). Механиче­ские свойства кровеносных сосудов определяются главным образом свойствами коллагена, эластина и гладких мышечных волокон. Со­держание этих составляющих сосудистой ткани изменяется по хо­ду кровеносной системы: отношение эластина к коллагену в общей сонной артерии 2:1, а в бедренной артерии 1:2. С удалением от сердца увеличивается доля гладких мышечных волокон, в артериолах они уже являются основной составляющей сосудистой ткани.

При детальном исследовании механических свойств сосудис­той ткани различают, каким образом вырезан из сосуда образец (вдоль или поперек сосуда). Можно, однако, рассматривать де­формацию сосуда в целом как результат действия давления из­нутри на упругий цилиндр.

Рассмотрим цилиндрическую часть кровеносного сосуда дли­ной l, толщиной h и радиусом внутренней части r. Сечения вдоль и поперек оси цилиндра показаны на рис. 8.22, а, б. Две половины цилиндрического сосуда взаимодействуют между собой по сечени­ям стенок цилиндра (заштрихованные области на рис. 8.22, а). Общая площадь этого «сечения взаимодействия» равна 2hl. Если в сосудистой стенке существует механическое напряжение а, то си­ла взаимодействия двух половинок сосуда равна

Эта сила уравновешивается силами давления на цилиндр изнутри (они показаны стрелками на рис. 8.22, б). Силы направлены под разными углами к горизонтальной плоскости (на рисунке). Для того чтобы найти их равнодействующую, следует просуммировать горизонтальные проекции. Однако проще найти равнодействую­щую силу, если умножить давление на проекцию площади полу­цилиндра на вертикальную плоскость ОО'. Эта проекция равна 2rl. Тогда выражение для силы через давление имеет вид

Приравнивая (8.10) и (8.11), получаем σ • 2hl = р • 2rl, откуда

Это уравнение Ламе.

Будем считать, что при растяжении сосуда объем его стенки не изменяется (площадь стенки возрастает, а толщина убывает), т. е. не изменяется площадь сечения стенки сосуда (рис. 8.22, б):

С учетом (8.13) преобразуем (8.12):

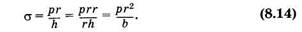
Из (8.14) видно, что в капиллярах (r→ 0) напряжение отсутст­вует (σ → 0).

В заключение отметим разделы и направления медицины, для которых особо важно иметь представление о пассивных механиче­ских свойствах биологических тканей:

— — — в космической медицине, так как человек находится в но­вых, экстремальных, условиях обитания;

— — — в спортивной медицине результативность достижений и ее возрастание побуждают портивных медиков обращать внимание на изические возможности опорно-двигательного аппарата человека; механические свойства тканей необходимо учитывать гиги­енистам при защите человека от действия вибраций; в протезировании при замене естественных органов и тка­ней искусственными также важно знать механические свойства и параметры биологических объектов;

— — — в судебной медицине следует знать устойчивость биологических структур по отношению к различным деформациям;

— — — в травматологии и ортопедии вопросы механического воз­ действия на организм являются определяющими.

Этот перечень не исчерпывает значения материала, изложен­ного в настоящей главе, для врачебного образования.

ГЛАВА 9 Физические вопросы гемодинамики

Гемодинамикой называют область биомеханики, в которой исследуется движение крови по сосудистой системе. Физи­ческой основой гемодинамики является гидродинамика. Те­чение крови зависит как от свойств крови, так и от свойств кровеносных сосудов.

В главе рассматриваются также физические основы работы некоторых технических устройств, используемых в связи с кровообращением.