Уравнение движения жидкости.

Слайд 1-13.

Теперь с учетом предыдущего сформулируем уравнение движения жидкости. Согласно второму закону Ньютона:

ускорения элемента жидкости ´ масса = сумме напряжений и массовых сил

Н

V(Н) p₁ Н Напряжение

So + DS

Р DН Р

Вес

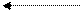
So

Напряжение

p₂

Хо Хо+DХ

Cлайд 1-13.Силы,действующие на прямоугольный элемент жидкости в потоке.

Пусть, например, элемент жидкости движется в направлении х в прямолинейном потоке, скорость в котором изменяется с координатой высоты Н, но не зависит от x и от времени.

Сила тяжести или вес направлена вниз.

Из баланса сил в вертикальном направлении следует, что при заданном х давление изменяется с высотой так же, как и в покоящейся жидкости и определяется уравнением:

p ₁ -p₂ = r DН g (1-13)

Рассмотрим теперь баланс горизонтальных сил.В отсутствие движения вязкие напряжения были бы равны нулю и давление на правой и левой гранях были бы одинаковы.

Но, как только появится движение, возникают вязкие силы. В данном примере они стремятся замедлить элемент, т.к. напряжение сдвига, направленное против движения, на нижней пов-ти элемента (S=So) больше,чем напряжение сдвига на верхней пов-ти ,направленное по движению (S =So + DS).

Для горизонтальной трубы составляющая веса в направлении движения равна нулю, и равномерный поток может осуществляться только, когда давление на одном конце трубы больше, чем на другом.

Для любого течения уравнение движения каждого эл-та может быть представлено в форме:

Масса´Ускорение = Массовая сила (вес) + Сила, обусловленная градиентом давления + вязкая сила.

Так как связь между вязкими силами и местными изменениями скорости известна (напряжение сдвига пропорционально скорости сдвига), это уравнение связывает градиент давления и массовую силу в любой точке с местной скоростью среды и скоростями ее изменения как во времени (ускорение), так и в пространстве (скорость сдвига). Очевидно, масса´ускорение в левой части есть сила инерции.

Лекция 1-2. Пуазейлевское течение в трубе.

слайд 1-14

Стационарное ламинарное течение жидкости может быть экспериментально реализовано на лабораторной установке, состоящей из длинной жесткой[ 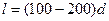; 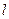- длина, 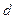- внутренний диаметр] цилиндрической трубки, соединенной с напорным и сливным резервуарами, в которых во время эксперимента поддерживаются постоянные давления ( 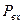и ).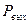

Напорный резервуар

Сливной резервуар

Рвх Рвых

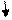К манометрам

Слайд 1-14. Эксперимент Пуазейля.

В стенке трубы проделаны через небольшие интервалы маленькие отверстия для измерения давления.

Давление на входе Рвх, а на выходе Рвых. Повышая давление на входе, т.е. увеличивая перепад Рвх-Рвых (Dр), мы увидим, чтообъемный расходQ тоже растет. При этом давление вдоль трубки сначала падает быстро (на 100 d),а затем уменьшается линейно с расстоянием.

Рвх

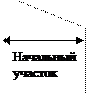Вход

Рвых

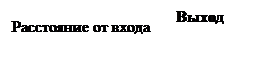Слайд 1-14. Падение давления на начальном участке .

Проведя подобные эксперименты с трубками разного диаметра,мы увидим,что при заданном градиенте объемный расход Q резко увеличивается с ростом диаметра, а именно пропорционален r⁴.

Кроме того,при увеличении вязкости для поддержания заданного постоянного расхода необходимо увеличить градиент давления.

На основании этого Пуазейль вывел знаменитый закон для стационарного потока, достаточно удаленной от ее начала:

Dp = 8 m LQ/p r⁴ или Q= Dp pr⁴ / 8 m L (1-14)

m- вязкость жидкости,

L- длина трубки

Таким образом, имеется три первичных фактора, определяющих сопротивление потоку крови: диаметр сосуда (или радиус), его длина и вязкость крови. При этом сопротивление сосуда (R) прямо пропорционально длине сосуда (l) , вязкости крови (m) и обратно пропорционально радиусу в 4 степени (r⁴)

R ~ L m / r⁴ (1-15)

Длина сосуда практически не изменяется внутри организма и поэтому может рассматриваться как константа. Вязкость обычно изменяется мало , однако, как мы покажем дальше, может значительно изменяться от гематокрита, температуры и скорости потока.

Зависимость между скоростью потока, радиусом и длиной сосуда показана на слайде .При этом принимается, что имеет место ламинарный поток, а давление, вязкость и длина сосуда являются константами.

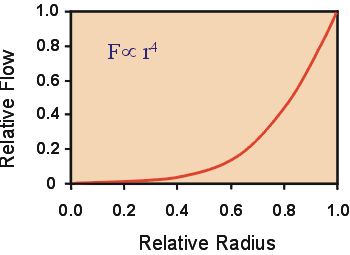
Слайд 1-14. Зависимость скорость кровотока – радиус сосуда.

Как видно уменьшение радиуса сосуда сильно влияет на поток и прямо пропорционально радиусу в 4 степени. Например, когда

радиус уменьшается только в 2 раза (0.5 относительный радиус)

поток уменьшается в 16 раз. Вновь сформированный поток будет составлять приблизительно 6% от исходного потока.

Заметим только, что формула (1-17) является примером решения уравнения Навье-Стокса для стационарного потока в прямой горизонтальной трубе круглого сечения со следующими дополнительными ограничениями:

1. Жидкость имеет гомогенную вязкость при всех скоростях сдвига

2. Трение жидкости у стенки намного больше внутреннего трения в жидкости и скорость жидкости у стенки равна нулю

3. Поток ламинарный

4. Поток стационарный-нет ускорений

5. Стенки трубки жесткие

Интересно, что гидравлическое уравнение Пуазейля можно переписать в терминах закона Ома, полагая, что давление – P-это напряжение-U,поток Q– ток Iи параметры трубки и жидкости (вязкость) 8 m l/pr⁴ –сопротивление R:

I = U/R Q=P/R; R=8 m l/pr⁴ = 8 m l/А² (1-16)

Распределение давления и формы профиля скорости вдоль трубки показаны на слайде 1-10. Длина начального участка трубки ( 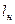), на котором происходит перестройка профиля скорости от плоского до параболического, может быть оценена неравенством: 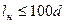, где 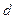- внутренний диаметр трубки. Участок,на котором давление падает быстро – называется начальным участком или областью входа.Поток за начальным участком называется полностью развитым.На этом участке градиент падает с расстоянием линейно и растет линейно с увеличением расхода.

Т. е. поток с параболическим профилем скорости (пуазейлевский поток) устанавливается только в прямой трубке на большом удалении от входа, а также от изгибов, сужений, ветвлений сосудов. Приняв, например, диаметр сосуда равным 5 мм, получим, что длина начального участка должна быть не менее 0.5 м. Вряд ли можно найти в сосудистой системе сегмент, удовлетворяющий всем перечисленным выше ограничениям. Тем не менее, описанная гидродинамическая модель пуазейлевского потока широко используется, напрмер, для лабораторной калибровки расходомеров крови в стандартных условиях пуазейлевского потока.

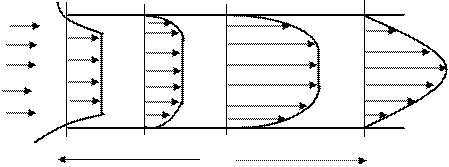Слайд 1-15. Развитие Пуазейлевского течения.

Физически эволюцию профиля скорости легко объяснить следующим образом. У самого входа все элементы жидкости движутся с одинаковой скоростью, и профиль скорости однородный или плоский. Однако та часть жидкости, которая соприкасается со стенкой трубки, полностью останавливается из-за прилипания на стенке. Немедленно устанавливается градиент скорости между неподвижной жидкостью у стенки и соседними элементами жидкости в ядре потока. По мере продвижения жидкости вдоль трубки вязкость все в большей степени видоизменяет начальный плоский профиль скорости. Исходно высокий градиент скорости у стенки становится меньше, а сдвиг охватывает все большую часть ядра потока. Следует иметь в виду, что как следствие закона сохранения масс центральная часть потока ускоряется с тем, чтобы объемный расход через любое сечение оставался постоянным. При этом , градиент скорости, который сначала был заметен около стенки, начинает проявляться на все больших расстояниях от нее. В конечном счете, скорость становится неодинакова по всему поперечному сечению трубки: она максимальна на оси и постепенно уменьшается по направлению к стенкам. Профиль скорости принимает вид параболы, устанавливается пуазейлевское течение. Когда этот полностью развитый профиль достигнут, он уже не меняется дальше вниз по течению.

Особенность ламинарного кровотока заключается в том, что чем крупнее частицы крови, тем ближе они располагаются к оси сосуда. В результате осевой поток крови почти целиком состоит из эритроцитов, образующих довольно компактный движущийся цилиндр с оболочкой из плазмы, содержащий мало клеток. Таким образом, средняя скорость кровотока выше, чем скорость тока плазмы.

Представление о пограничном слое.

Слайд 1-15.

Как мы уже отмечали, вязкая сила торможения, с которой стенка действует на прилегающий к ней слои жидкости, последовательно передается все более удаленным слоям. Это обусловлено наличием вязкости.

У входа толщина слоя чрезвычайно мала и за пределами этого слоя профиль скорости практически плоский и влияние вязкости незначительно. Далее вниз по течению толщина слоя, в котором проявляется вязкость, возрастает и этот слой называется пограничным.

Толщина пограничного слоя растет вдоль трубки как корень квадратный расстояния от входа Х ^½^.

С увеличением расхода или скорости свободного потока толщина пограничного слоя уменьшается и увеличивается с ростом вязкости.

На более удаленном расстоянии пограничный слой заполняет всю трубку и устанавливается Пуазейлевское течение.

В этом случае его толщина становится равной радиусу трубки d/2 при длине начального участка Х:

X = k’d² U/n или k’ d (Ud/n ) (1-17)

Величина U d/n называетсячислом Рейнольдса (Re),о котором мы поговорим позже.

k’ –константа,равная 0,03 найдена экспериментально

Таким образом, длина начального участка для стационарного потока задается выражением:

X = 0,03 d Re (1-18)

Для трубки d= 2см длина начального участка при числе Re = 1000 составит 60 см – это значение характерно для аорты человека ,конечно, при условии, что аорта-прямая трубка, а поток в ней – стационарный и имел скорость 20см/сек.

Следует отметить ,что данное выражение удовлетворительно предсказывает длину начального участка при значениях числа Рейнольдса в интервале 10 – 2500.

Число Рейнольдса.

Подробнее остановимся на числе Рейнольдса и попробуем понять его физический смысл.

При анализе баланса сил, действующих на элемент жидкости, мы обращали внимание на отношение величин инерционных и вязких сил.

Отношение инерционных и вязких сил – является важной характеристикой всех течений жидкости.

Для потока в трубке характерными величинами скорости и размера системы являются линейная скорость U и диаметр d.

Поэтому можно сказать, что вязкие силы могут быть определены как произведение вязкости на скорости сдвига:

вязкие силы=m U/d.

С другой стороны, инерционная сила пропорциональна кинетической энергии единичного объема жидкости (rU²).

Тогда относительная значимость этих двух величин может быть оценена как

Число Рейнольдса=Инерционные силы /Вязкие силы =

rU² / m (U/d) или = Ud/n (1-19)

n-кинематическая вязкость (m/r).

Если подставить размерности в данное уравнение, то можно увидеть что число Рейнольдса Re является безразмерной величиной.

КогдаRe <<1 вязкие силыпреобладают, инерционные силы пренебрежимо малы (например, на уровне микрососудов, где течение рассматривается как чисто вязкое).

Когда>>1 ,преобладают инерционные силы, а вязкость лишь незначительно изменяет характер течения. Примерами такой ситуации служат течения в крупных артериях и венах.

В типичной человеческой аорте можно вычислить число Рейнольдса, полагая, что диаметр аорты 2.5 см и среднее скорость 20 мл/с

( при сердечном выбросе 6 л/мин) и оно составляет 1500.

Для этих расчетов полагали, что плотность цельной крови равна 1.056 г/СС, а коэффициент вязкости 3.5 сП.

Таким образом, среднее число Рейнольдса ниже критической величины около 2500.Однако, в течение систолического пика, если скорость потока в пике 20 л/мин число Рейнольдса может достигать 5100. Тем не менее человеческая аорта является эластичным сосудом и имеет сложную геометрию и поэтому критическое число Рейнольдса, определяемое из экспериментов с прямой жесткой цилиндрической трубкой, не может быть применимо для данной ситуации. С другой стороны, и нет экспериментов, подтверждающих турбулизацию потока в системе кровообращения в норме, при отсутствии таких нарушений, как клапанные или артериальные стенозы. Следовательно, предположение ламинарного потока в аорте можно считать корректным.

<1 2 345 6 7 >

Дата добавления: 2016-08-06; просмотров: 2447;