Система единиц (SI)

.

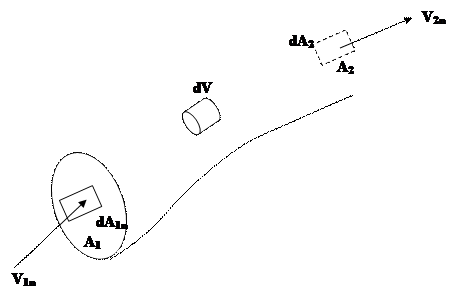Слайд 1-6. Баланс сил в потоке жидкости

Принятые допущения

а) v₁ и v₂ постоянны в сечениях 1 и 2 и нормальны к ним.

b) Поток стационарен и объем трубки постоянен во времени.

A₁ v₁ =A₂ v₂ =Q ( константа) (1-2)

Q – объемный расход в (м³/с)

Слайд 1-7. Данный принцип исходит также из несжимаемости воды и крови. Еще одним важным условием является жесткость трубок, по которым течет жидкость.

В случае нежестких трубок, масса втекающая – масса, вытекающая = скорости изменения массы внутри трубки

∫ ρ v_1n dA -∫ ρ v_2n dA = - ∂/∂t ∫ ρ dV (1-3)

А₁ А_{2 V}

Т.е в растяжимой трубке подобной аорте в каждый момент величина (V₁A₁-V₂A₂) равна скорости увеличения объема между двумя плоскостями.

Скорость v₁ Скорость v₂

Площадь А₁ Площадь А₂

К закону сохранения массы

Если скорости отличаются в сечениях, то

V₁ = 1/ A₁ ∫ v ₁ dA

V₂= 1/ A₂ ∫ v ₂ dA ( 1-4)

Q = A₁ V₁ =A₂ V₂ (1-5)

В случае стационарного потока объемный расход будет одинаков во всех частях даже растяжимой трубки.

Количественной характеристикой течения крови является линейная скорость кровотока, то есть скорость перемещения малого объёма крови, размер которого намного меньше диаметра сосуда.

Для интегральной характеристики процесса массопереноса через данное сечение сосуда используют среднее значение линейной скорости 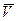, либо среднее значение объёмной скорости 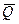(его иногда кратко называют расходом), которые связаны соотношением:

Q =V S (1-6) ,

где 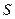– площадь поперечного сечения сосуда.

Из условия непрерывности потока следует, что для участка сосуда без источников и стоков 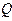= const, в то время как 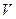изменяется обратно пропорционально .

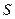Очевидно, что количество крови, притекающей по артериям к какому – либо органу в единицу времени, в среднем равно количеству крови, оттекающей от него по венам; при этом средняя по сечению скорость кровотока в артериях существенно зависит от времени в течение сердечного цикла, а в венах практически постоянна на том же интервале времени. То есть венозный кровоток является стационарным (не пульсирующим), а артериальный – нестационарным (пульсирующим).