Слайды 1-9,1-10. Примеры теоремы Бернулли
Реология крови
Реология это изучение деформации и течение материала. Объект или тело деформируются, если его форма и размер изменяются под воздействием сил. Если степень деформации изменяется постоянно со временем, то тело рассматривается как жидкость. Данная тема посвящена поведению крови при ее течении по сосудам. Основа понимания реологических характеристик крови как жидкости in vivo при нормальных условиях поможет нам определить границы эффектов ненормальных условий потока таких, как влияние стеноза клапанов, стеноза сосудов на форменные элементы крови. Понимание динамики потока в таких устройствах как протезы клапанов сердца, сосудистые протезы и искусственное сердце и влияния условий таких потоков на кровь также поможет нам улучшить конструкции имплантатов. Кроме того, широко используются в медицине и некоторые экстракорпоральные устройства такие, как оксигенатор крови, диализные машины и вспомогательные насосы. Поэтому понимание поведения потока крови в таких устройствах также поможет нам в улучшении конструкций этих устройств так , чтобы минимизировать травму крови и улучшить функционирование этих устройстввы механики жидкостей .
Жидкость или газ деформируются под воздействием сдвиговых напряжений. В покое жидкости не имеют сдвиговых напряжений.
Мы рассматриваем жидкость как сплошную непрерывную среду. В макроскопической шкале характеристики жидкости описываются такими параметрами как плотность, температура, давление и т.д.
Рассмотрим основные свойства жидкости:
· Плотность
· Вязкость
· Поверхностное натяжение
· Сжимаемость
Плотность
r = Масса/Объем (кг/м3)
ρ воды= 999 кг/м3 при 15о С
ρ воздуха = 1.22 кг/м3 (при стандартном атмосферном давлении)
ρцельной крови = 1060 кг/м3 (6% выше, чем воды)
Удельный вес , S = плотность жидкости / плотность воды
Для цельной крови S = 1.06
Понятие вязкости.
Слайд 1-11.
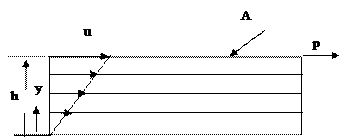
Как мы уже говорили, жидкость может определяться как субстанция, которая постоянно деформируется при воздействии сдвиговых или тангенсальных напряжений. Рассмотрим две параллельные плоскости в поперечном сечении А см 3.
 |
Слайд 1-11.
Тангенсальная сила Р приложена к верней плоскости , как показано на слайде. В результате она будет сдвигать эту плоскость со скоростью u (cм/с) по отношению к нижней плоскости. Слои жидкости, прилегающие к верхней плоскости , будут двигаться с той же скоростью, как и верхняя плоскость, т.к. полагаем, что жидкость не проскальзывает относительно плоскости. Аналогично жидкость, прилегающая к нижней плоскости, останется в покое.
Однако, появляется, как видно, градиент скорости. Сдвиговая сила Р, деленная на площадь А, определяется как сдвиговое напряжение (shear stress) τ.
Градиент скорости определяется как скорость сдвига (rate of shear) γ.
Т.е.γ – есть отношение u/h , где h– расстояние между двумя параллельными плоскостями.
Скорость сдвига выражается в размерности с-1 .
В пределе скорость сдвига определяется в пределе как du /dy , как показано на слайде, где y - расстояние перпидикулярное направлению сдвига.
Тангенсальное напряжение во многом аналогично силе трения, которая противодействует относительному перемещению соседних слоев жидкости.
Поэтому, когда жидкость течет над плоской поверхностью и ее более удаленные от стенки слои ,движутся быстрее, чем близлежащие, а тангенсальная составляющая напряжения, действующая между соседними слоями, стремится замедлить движение более быстрых из них и ускорить движение более медленных.
Ньютон назвал это тангенсальноенапряжение - “дефектомскольжения“. Теперь это свойство называют вязкостью.
Свойства потока всех жидкостей определяются как зависимость между напряжением сдвига и скоростью сдвига. Жидкости, в которых напряжение сдвига прямо пропорционально скорости сдвига называются Ньютоновскимижидкостями.
τ =μ γ (1-9)
где μ – коэффициент пропорциональности, определяемая как коэффициент вязкости.
Таким образом, вязкость жидкости или внутреннее трение – свойство жидкости оказывать сопротивление перемещению одной ее части относительно другой. В свою очередь вязкость жидкости обусловлена, в первую очередь, межмолекулярным взаимодействием (например, силами Ван-дер-Ваальса, ограничивающим подвижность молекул). Наличие вязкости приводит к диссипации энергии внешнего источника, вызывающего движение жидкости, и переходу ее в теплоту.
В определенных диапазонах напряжений и скоростей сдвига кровь является неньютоновской жидкостью, т.к. ее вязкость изменяется в определенных скоростях сдвига. В крупных сосудах кровь можно считать ньютоновской жидкостью и описание ее движения может быть упрощено. Однако в мелких сосудах, где размер элементов крови соизмерим с диаметров сосудов, подобное упрощение невозможно.
Поскольку напряжение, как и давление, равно силе на единицу поверхности, а градиент скорости – величина, обратная времени и измеряемая в с –1,то из уравнения следует, что вязкость в системе СИ измеряется в H·c·м -2 или Па· с (Па=Н· м-2)
Часто вязкость крови обозначают в Пуазах в честь Пуазейля (1 Пуаз = 0.1 Па· с) или сантиПуазах (1 сПз = 0.01 Пз).
В норме значения динамической вязкости крови лежат в пределах 3-4 сПз.
(Слайд 1-12).Зависимость, выраженная уравнением 1.9, может быть построена в виде графика напряжение сдвига – скорость сдвига
 | |||
|
Слайд 1-12
Как видно из графика,ньютоновская жидкость представляется прямой линией, проходящей из начала координат с наклоном μ.К сожалению, все жидкости не следуют этой идеальной линейной зависимости и все они, в общем, классифицируются как неньютоновские жидкости. В этих жидкостях отношение напряжения сдвига к скорости сдвига в любой точке называют кажущейся вязкостью и она может сильно отличаться при разных скоростях сдвига.
Неньютоновские жидкости, описываемые нелинейностью и представленные кривой, выходящей из начала координат можно представить уравнением:
τ =к γ n (1-10) ,
где n ≠ 1.
Такие жидкости классифицируются как жидкости со степенным законом или power law fluids.Другой класс жидкостей, известные как Bingham пластики, которые сопротивляются деформации при приложении напряжения сдвига, пока оно не превысит пороговое напряжение (yield stress), за которым наблюдается линейная зависимость напряжения сдвига и скорости сдвига (Bingham пластики)
τ = τy + μ b γ (1-11)
где τy – пороговое напряжение и μ b – пластическая вязкость.
Жидкости, которые имеют пороговое напряжение и имеют нелинейную зависимость напряжения сдвига-скорости сдвига , называют Casson’s жидкостями.
Наилучшее эмпирическое выражение, описывающее такие жидкости и известное как уравнение Casson’s , приведено ниже
|
= τ у + k c γ (1-12)
Как указывалось ранее важно знание реологических свойств крови является, чрезвычайно важным для конструирования устройств, по которым протекает кровь. Для того чтобы понимать зависимость между напряжением сдвига и скоростью сдвига для крови, необходимо провести некоторые экспериментальные измерения.
Но об этом поговорим немного позже.
А сейчас отметим также, что вязкость жидкости сильно зависит от температуры. В целом вязкость жидкости уменьшается с увеличением температуры, в то время как вязкость газов увеличивается с ростом температуры.
Дата добавления: 2016-08-06; просмотров: 1067;
Поиск по сайту
Узнать еще
Публикации по технике и механике
Публикации по биологии
Публикации по информатике
Публикации по строительству
Публикации по физике
Публикации по химии
Публикации по электронике
Публикации по искусству
Публикации по истории
