Слайд 1-17. Потери энергии при стенозе сосуда.

<2 3 4 567 8 >

Очевидно, что на длине трубы произойдет падение давления (PЕ – потенциальная энергия) согласно уравнению Пуазейля. Полная энергия уменьшится на ту же величину, поскольку кинетическая энергия (КЕ) вдоль трубки остается неизменной. ( Линейная скорость потока V не изменяется)

Ситуация сильно изменится в сосуде, где имеется стеноз или сужение сосуда. Например, мы имеем сужение радиуса на 50%.В результате скорость возрастет в месте сужения в 4 раза (согласно Пуазейлю скорость обратно пропорциональна квадрату радиуса (r²),а увеличение скорости вызовет 16-кратное увеличение кинетической энергии КЕ (т.к. последняя µ V²).И если, например, КЕ на трубке без сужения была равна 2 мм. рт.ст.,то теперь при стенозе в 50% она будет 32 мм.рт.ст. Это приведет к уменьшению полной энергии Е в области стеноза, несмотря на увеличение кинетической энергии из-за чрезмерных потерь на трение

( потенциальная энергия уменьшится на 40%). В постстенозном сегменте скорость снова вернется к прежней величине.

Интересно, что давление в конце сегмента (РЕ) выше, чем в на участке стеноза.

Таким образом, все это иллюстрирует очень важный принцип, о котором мы уже упоминали (принцип Бернулли). Кровь, протекая с высокой скоростью, будет иметь высокое отношение кинетической энергии к потенциальной (давлению). При выбросе крови из левого желудочка с высокой скоростью кинетическая энергия , которая наблюдается в восходящей аорте, может быть значительной особенно во время физических упражнениях , когда скорость кровотока может увеличиваться в несколько раз.

Рассмотрим еще один интересный феномен в сердечно-сосудистой системе, а именно давление крови в аневризме, например, аорты. Сама по себе аневризма вызвана слабостью сосудистой стенки и в этом месте происходит выпячивание сосуда, и полное поперечное сечение сосуда значительно увеличивается. Анализ показывает, скорость потока в аневризме значительно уменьшается, и кинетическая энергия преобразуется в этом месте в потенциальную энергию и давление в аневризме увеличивается. Даже если увеличение давления незначительно в состоянии покоя, то при физических упражнениях, когда скорость потока значительно увеличивается, соотвествуещее преобразование кинетической энергии в потенциальное давление в области аневризмы может быть значительным, что может вызвать дальнейшее расширение поперечного сечения сосуда и привести к его разрыву. (слайд1-18).Есть еще одно практическое применение принципа Бернулли при измерении давления крови внутри восходящей аорты. Учитывая, что при выбросе крови из аорты кинетическая энергия очень высокая, величина измеряемого давления внутри аорты будет различной в зависимости от того, как мы измеряем давление. Как известно, общий метод клинического измерения внутрисосудистого давления является введение катетера, заполненного жидкостью в сосуд и соединение его с датчиком давления. При этом нужно учитывать при таком измерении давления эффект влияния кинетической энергии. Если датчик или катетер расположен против потока (E),он будет измерять давление значительно более высокое, чем датчик или катетер, измеряющий боковое давление (S) И причина этого несоответствия состоит в том, что датчик, установленный против тока, измеряет полную энергию потока. Когда поток “ударяет” по концу катетера, кинетическая энергия преобразуется в потенциальную (давление) энергию и добавляется к потенциальной энергии, отражая полную энергию. В свою очередь при боковом расположении катетера поток не ударяет по нему и кинетическая энергия не превращается в потенциальную (давление). Т.е. он будет измерять только потенциальную энергию, действующую в аорте. Разница между двумя типами измерений может изменяться от нескольких мм.рт.ст. до более 20 мм.рт.ст.При этом, эта разница между измерениями может быть особенно значительной в сегментах суженных сосудов, где кинетическая энергия высока.

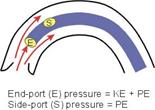
Слайд1-18.Измерение давления в аорте

Понятие турбулентности

Слайд 1-19

Турбулентное течение возникает при гладком течении, когда ламинарный поток разрушается. В сердечно-сосудистой системе это происходит в области сужений сердечных клапанов или артериальные русла, в местах разветвления сосудов, а также в аорте при резком увеличении кровотока во время физических упражнений. Рейнольдс опубликовал результаты экспериментов в 1883г. Он измерял градиент давления вдоль трубки и увидел, что градиент давления при низких скоростях пропорционален расходу (что и следует ожидать из закона Пуазейля), а при более высоких пропорционален квадрату расхода. Начало турбулентного течения может быть предсказано, вычисляя число Reynolds (Rе), которое, как мы видели, равно:

Re = rUd/m (1-22)

Повтор: Что такое числоRe =инерционные силы ρU ² /вязкие силы μ(U/d) = Ud/ν

Обратить внимание наm в знаменателе , т.е. чем менее вязкая среда, тем вышеRe.

Как мы уже говорили, имеется понятие критического числа Re , при превышении которого ламинарный поток разрушается и начинается турбулентное течение.

Поэтому, когда скорость крови увеличивается в сосудах или через клапаны, нет постепенного увеличения в турбулизации, когда число Рейнольдса увеличивается. Вместо этого, как только ламинарный поток достигает критического числа Рейнольдса, с этой точки и развивается турбулизация потока. При идеальных условиях (т.е. длинные, прямые и гладкие сосуды) критическое число относительно высоко и может достигать 10000 . Однако у мест разветвления сосудов или в сосудах с атеросклеротическими отложениями критическое Re намного ниже и турбулизация может возникнуть уже при нормальных физиологических скоростях уже при числах Re=1000 -1200.

Во время периода изгнания крови из сердца в проксимальных отделах аорты и легочного ствола число Рейнольдса намного превышает это критическое значение, и поэтому поток в данных областях сосудистого русла может стать турбулентным. При возрастании скорости кровотока (например, при мышечной работе) или снижении вязкости крови (например, при резко выраженной анемии) течение может стать турбулентным во всех крупных артериях.

Важно обратить внимание, что уменьшение диаметра приводит к непропорциональному увеличению средней скорости, а именно, как мы помним, обратно пропорциональна квадрату радиуса ( по Пуазейлю)

Например, если артериальный стеноз уменьшает диаметр сосуда на 50 %, средняя скорость увеличится в 4 раза, значительно приближая Re к критической величине ( см.слайд слева). Помимо увеличения Re , увеличение скорости приводит к увеличению кинетической энергии, которая, в свою очередь, может вести к уменьшению в потенциальной энергии (эффект Бернулли ), даже к отрицательному давлению, что может привести к коллапсу сосуда и при определенных обстоятельствах к колебаниям (пульсациям) в сосуде. А это в еще большей степени будет способствовать турбулизации потока !!.

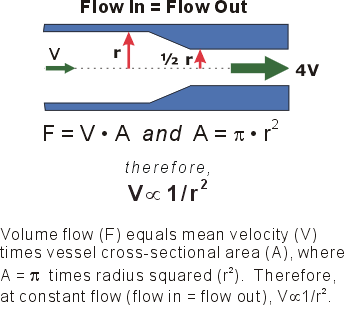
Слайд 1-19.Поток крови в местах сужения (стеноз артерии)

Турбулизация отмечается характеристическими шумами в момент выброса крови, которые можно услышать обычным стетоскопом. Даже просто само по себе увеличение сердечного выброса даже через анатомически нормальный клапан может вызвать эти шумы из-за турбулизации потока. Иногда подобный шум можно слышать у беременных женщин при увеличении сердечного выброса вследствие анемии. Для турбулентного течения характерно наличие завихрений, в которых частички жидкости перемещаются не только параллельно оси сосуда, но и перпендикулярно ей. Эти завихрения существенно увеличивают внутреннее трение жидкости, и профиль течения уплощается!! Турбулизация также вызывает увеличение потери энергии и более высокому падению давления по сравнению с пуазейлевским течением. Поэтому, как показано на слайде, если кровоток увеличивается в 2 раза через стенозированный сосуд, падение давления в этом участке может увеличиться в 3-4 раза по сравнению с двукратным увеличением падения давления при ламинарном пуазейлевским потоке. Здесь показано в сравнении падение давления в местах сужения артерий при ламинарном и турбулентном течении. . Как видно, для создания данного потока требуется большее давление. Как следствие этого, нагрузка на сердце при турбулентном кровотоке значительно увеличивается !!.

Таким образом, турбулизация изменяет отношения между потоком и давлением так, что оно становится нелинейным, а не пропорциональным как в случае ламинарного потока.

Если визуализировать турбулентный поток с помощью введения в него струйки красителя, можно наблюдать, что на входе в трубку профиль скорости будет плоский, а все элементы жидкости движутся с одинаковой скоростью. На небольшом расстоянии от входа под действием вязких сил происходит некоторое изменение профиля, но турбулентность еще осутствует. Затем ниже по течению непрерывность потока внезапно нарушается, и поток становится турбулентным. Причем первыми разрушаются струйки, проходящие по краю пограничного слоя, а через небольшое расстояние разрушаются струйки внутри пограничного слоя и в ядре потока.

При этом ядро потока имеет гораздо более плоский профиль по сравнению с ламинарным потоком. Максимальная скорость, наблюдаемая у оси примерно в 1.2 раза выше средней по течению скорости.( При параболическом ламинарном профиле скоростей это составляет 1,6)

Длина начального участка для турбулентного потока меньше, чем для ламинарного и ее можно оценить из следующего соотношения:

X = 0,693 dRe ^1/4 . (1-23)

Экспериментально определяемыми признаками наличия турбулентности в потоке жидкости или газа являются высокочастотные флуктуации направления и модуля вектора скорости потока в какой-либо выбранной точке. Обычно для того чтобы измерить эти флюктуации, не нарушая структуру потока необходимо пользоваться датчиком, имеющим малый измерительный объем и достаточное частотное разрешение. В качестве такого датчика используется проволочный или пленочный термоанемометр.

И еще несколько замечаний по поводу турбулентности.

· Турбулентность не развивается, пока Re не достигнет значения много большего, чем обычное критическое значение , в аорте ~2300.

· Турбулентность сохраняется при уменьшении скорости потока, даже когда Re становится ниже критического !!. Отчасти это определяется конечным временем, необходимым для затухания вихрей.

· И последнее – возникновение турбулентности в пульсирующем потоке определяется не только пиковым значением Re.Для того, чтобы возмущение потока при сверхкритических Re превратилось в турбулентность, необходимо некоторое конечное время. А при высокой частоте сокращений сердца длительность одного пульсового цикла может оказаться недостаточной для перехода к турбулентному течению даже при критических Re. Поэтому, чтобы обобщить вышесказанное о факторе времени, играющего огромное значение для пульсирующего потока, рассмотрим некоторые положения, связанные с отличием стационарного потока, имеющего место только в области мелких вен, от нестационарного, практически имеющего место во всех артериях и крупных венах.

Нестационарное течение в очень длинной трубке.

До сих пор, рассматривая ламинарное течение, мы полагали, что на входе гипотетической трубки действует постоянное давление.

На практике в сердечно-сосудистой системе поток, выходящий из сердца пульсирующий и течение, возникающее при этом, можно назвать нестационарным.

Слайд 1-20.

Рассмотрим процессы, возникающие в очень длинной прямой трубке, если к жидкости приложен медленно колеблющийся градиент давления.

При этом течение будет замедляться, останавливаться, изменять свое направление, ускоряться в новом направлении и снова замедляться.

Когда это происходит достаточно медленно, то течение в каждый момент будет характеризоваться параболическим профилем скорости. Однако с увеличением частоты колебаний профиль скорости постепенно искажается. Инерция не позволяет жидкости в центральной части потока двигаться синхронно с приложенным давлением, наблюдается запаздывание, величина которого растет с увеличением частоты колебаний давления. В тоже самое время амплитуда движения в ядре уменьшается.

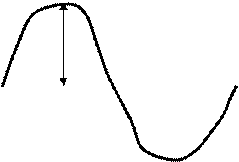
Рассмотрим простейшую форму колебаний давления-синусоидальную, т.е. к трубе приложено давление, которое изменяется по синусоидальному закону:

DP_t = DPо sin wt (1-24)

Где w -угловая частота (w= 2pf , f - частота колебаний)

DP_t

DP₀

+ T (время)

-DP₀

Т=2 p/w- период

Слайд 1-20. Пульсирующее давление

Таким образом, мгновенный градиент давления изменяется во времени следующим образом: в момент t= 0 он равен нулю; далее DP_tрастет до максимальной величины DPо, затем падает до нуля, становится отрицательным и уменьшается до величины - DPо. После чего вновь начинает расти и проходит через нуль и цикл повторяется. Период времени Т, на протяжении которого происходит один цикл колебаний, равен 2 p/w.

Cлайд 1-21.

Для характеристики такого потока весьма полезным безразмерным параметром является число Уомерсли a,показывающее, как сильно отличается пуазейлевский профиль скоростей при ламинарном течении в длинной трубке от профиля скоростей при синусоидальном воздействие давления с частотой w:

a = d/2 Ö w/n (1-25)

гдеd –диаметр,n=m/r-кинематическая вязкость.

Данный параметр aиногда называютчислом Рейнольдса для нестационарного потока, поскольку он характеризует отношение вязких и инерционных сил.

При низких значениях a<1 –течение можно считать квазистационарным.При этом в каждый момент времени профиль скорости параболический, а расход определяется мгновенным значением градиента давления, в течении преобладают вязкие силы, а инерционностью можно пренебречь.

При более высоких значенияхa мгновенный профиль скоростей искажается из-за большего влияния инерционных сил. Поток запаздывает по отношению к приложенному градиенту давления.

1 Qmax/Q стац

0.8

0.6

0.4

0.2 a

0 1 2 3 4 5 6 7 8 9 10

20⁰

40⁰Запаздывание по фазе

60⁰

Слайд 1-21.Изменение амплитуды и фазы потока при синусоидальном градиенте с увеличением параметра a.

Здесь представлено изменение амплитуды и фазы колебательного потока при синусоидальном градиенте давления с увеличением параметра a. При этом амплитуда характеризуется отношением максимального мгновенного расходаQmaxк стационарному расходуQ стац,который бы установился бы при максимальном (соответствующем амплитудному значению градиента давления) перепаде давления на трубке.

При малых значениях a величина расхода Qt определяется мгновенным градиентом давления Dр_t в соответствие с законом Пуазейля:

Qt=Qст sin( wt) (1-26)

При более высоких a(в диапазоне 1-3) мгновенный расход отстает от мгновенного градиента давлений на время j/w и уравнение принимает вид:

Qt=Qст sin( wt -j ) (1-27)

Т.е. расход в данный момент определяется через градиент давления со сдвигом по времени t-j/w,в то время, как амплитуда меняется мало.При еще более высоких a ( > 4) в потоке преобладают инерционные силы, причем , что при этом не только увеличивается отставание по фазе, но и существенно уменьшаются пиковые значения расхода по сравнению с величиной Qст, предсказываемой законом Пуазейля.

В системе кровообращения величины a, рассчитанные для частоты сокращения сердца, изменяются в широком диапазоне: в аорте aможет быть > 10,тогда как в капиллярах составляет 0.001.

<2 3 4 567 8 >

Дата добавления: 2016-08-06; просмотров: 1719;