Лекция 5. Линейные дифференциальные уравнения с постоянными коэффициентами. Метод Эйлера и метод подбора вычисления частных решений неоднородных уравнений

На предыдушей лекции были приведены примеры линейно независимых систем функций. Сделано это было не случайно, так как именно такие функции образуют фундаментальные системы решений дифференциальных уравнений с постоянными коэффициентами. Уравнения такого типа могут быть изучены полностью, если будут найдены корни соответствующих характеристических многочленов (см. ни же ). Построению корней этих многочленов (их называют характеристическими числами) и связи характеристических чисел с решениями дифференциальных уравнений уделяется основное внимание в настоящей лекции.

1. Метод Эйлера построения общего решения однородного дифференциального уравнения с постоянными коэффициентами в случае простых корней характеристического уравнения

Рассмотрим уравнение

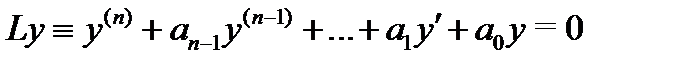
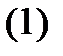
с постоянными коэффициентами 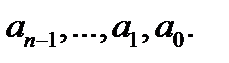Построим по нему алгебраическое уравнение

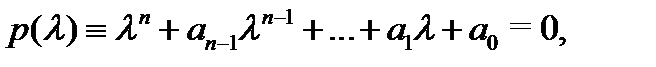
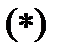
заменив в (1) производные 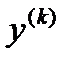на степени ( ).

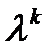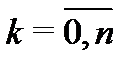Определение 1. Многочлен 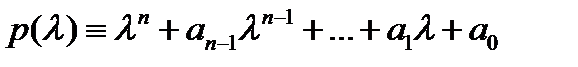называется характерис-

тическим многочленом уравнения (1), а само уравнение 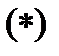– характеристическим уравнением, соответствующим уравнению (1).

Имеет место очевидное тождество

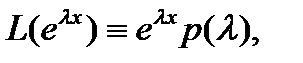
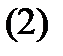
если 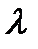– постоянная, так как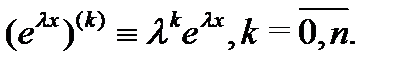

Теорема Эйлера. Для того чтобы экспонента 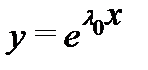( 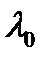– постоянная) была решением уравнения (1), необходимо и достаточно, чтобы 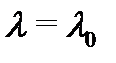было корнем характеристического многочлена 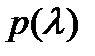(или, что то же самое, корнем характеристического уравнения ).

Доказательство.Действительно, если 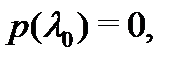то из (2) следует тождество 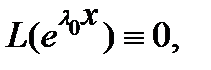показывающее, что экспонента 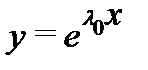является решением уравнения (1). Обратно: если 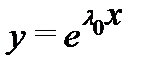– решение уравнения (1), то 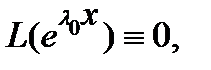и из (2) следует, что 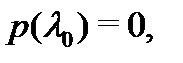т.е. 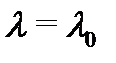– корень характеристического многочлена 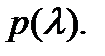Теорема доказана.

Из теоремы Эйлера сразу же вытекает следующий результат.

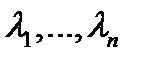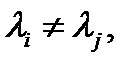
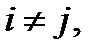
Теорема 1. Если все корни характеристического уравнения различны (т.е. 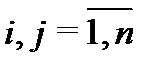), то система функций

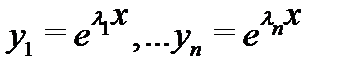
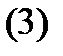
образует фундаментальную систему решений уравнения (1). В этом случае общее решение (на любом отрезке [a,b]) уравнения (1) имеет вид

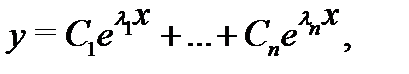
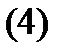
где 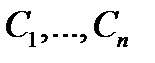– произвольные постоянные.

Доказательство следует сразу из теоремы Эйлера и утверждения предыдущей лекции.

Общее решение (4) уравнения (1) может быть комплексным, если хотя бы один из корней 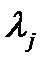характеристического полинома 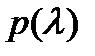комплексный. Для уравнений (1) с действительными коэффициентами 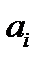принято записывать общее решение в действительной форме. Это нетрудно сделать, если воспользоваться утверждением 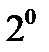лекции 4 и отделив в комплексном решении 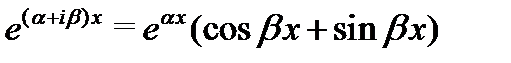мнимую и действительную част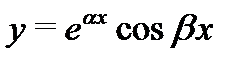и: и 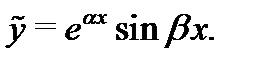Согласно действительные функци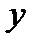и и 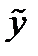также являются решениями однородного уравнения (1) с действительными коэффициентами. Поступив так с каждой комплексной экспонентой в 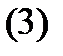, получим следующий результат.

Теорема 2. Пусть корни 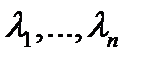характеристического уравнения различны, а коэффициенты 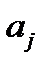уравнения (1) действительны. Пусть, далее, корни 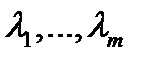–действительны, а остальные корни 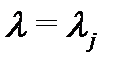комплексны:

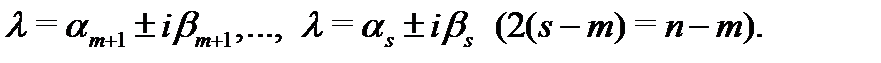
Тогда фундаментальную систему решений уравнения (1) можно выбрать в виде действительных функций

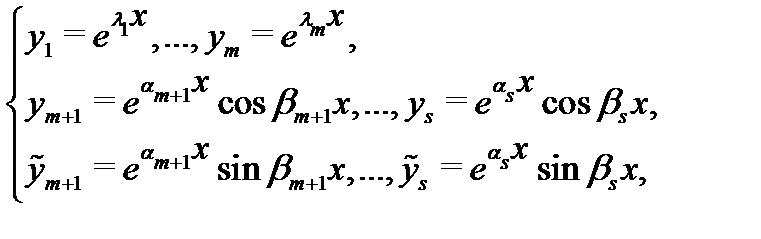
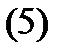
а общее решение уравнения (1) записать в виде

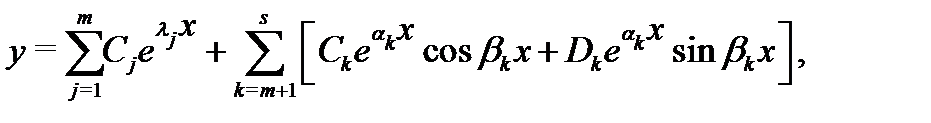
где 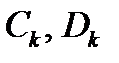– произвольные постоянные.

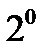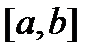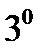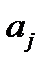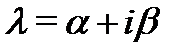Доказательство следует из того, что функции (5) являются решениями уравнения (1) (лекция 4, утверждение ) и образуют линейно независимую систему на любом отрезке (лекция 4, утверждение ). Остаётся заметить, что в силу действительности всех коэффициентов уравнения (1) его характеристическое уравнение наряду с корнем имеет и комплексно-сопряженный корень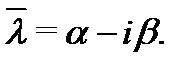

Пример 1. Найти общее решение уравнения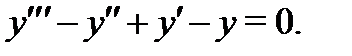

Решение. Составим характеристическое уравнение :

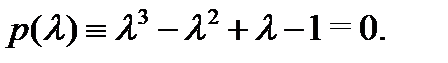
Разлагая его левую часть на множители, будем иметь

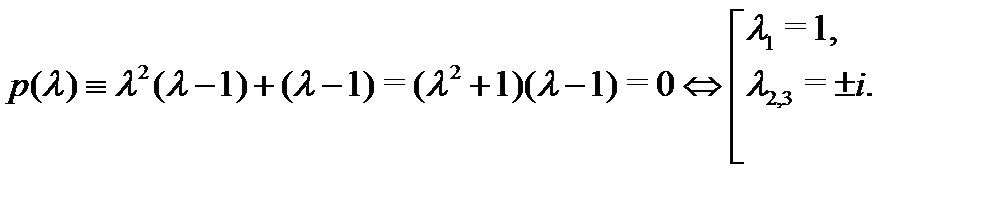
Итак, все корни характеристического уравнения различны. Согласно теореме 1 соответствующая фундаментальная система решений будет иметь вид

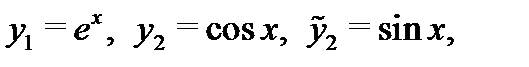
а значит общее решение исходного уравнения запишется в форме

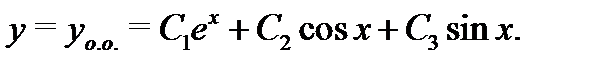
2. Построение общего решения однородного дифференциального уравнения в случае кратных корней характеристического уравнения

Напомним сначала, что корень 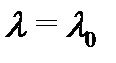характеристического многочлена 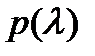называется корнем кратност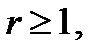и если

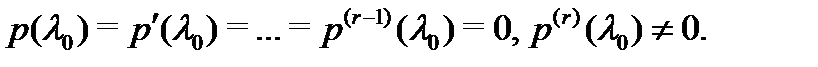
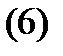
Полезно заметить, что если полином 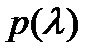имеет 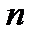различных корней 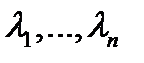( 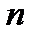– степень многочлена 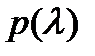), то все они имеют кратность 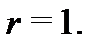Однократные корни называют еще простыми корнями .

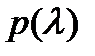Записав для многочлена 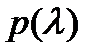формулу Тейлора

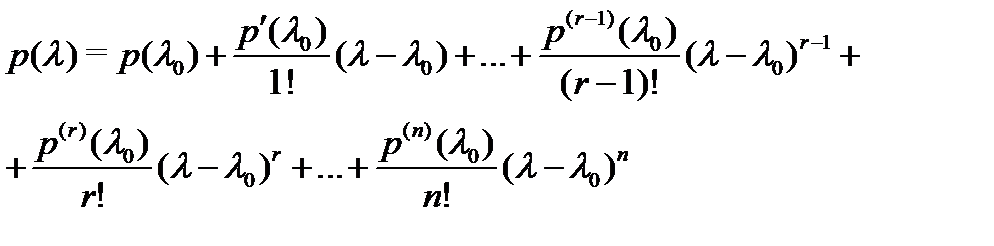
(остаточный член его равен тождественно нулю), получим с учетом равенств (6), что если 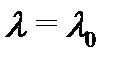– корень кратности 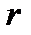, то 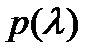представляется в виде

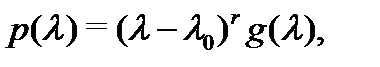
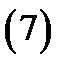
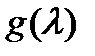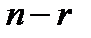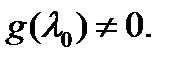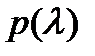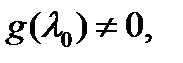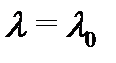где – многочлен степени такой, что Очевидно, верно и обратное: если представляется в виде (7) , где то –- корень кратности 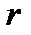многочлена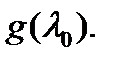

Построению фундаментальной системы решений в случае кратных корней характеристического уравнения предпошлем несколько вспомогательных утверждений.

Если 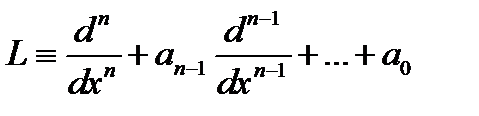– дифференциальный оператор с постоянными коэффициентами 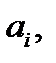то имеет место формула

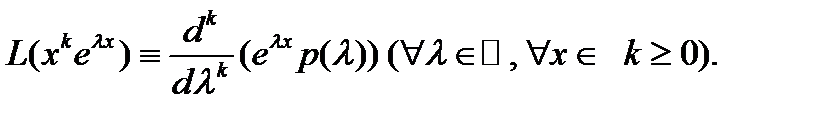
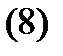
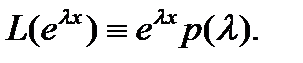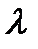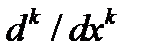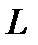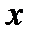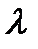Действительно, по (2) имеем Дифференцируя это тождество по и учитывая, что операторы и перестановочны при применении их к бесконечно дифференцируемой по и функции 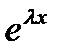, будем иметь

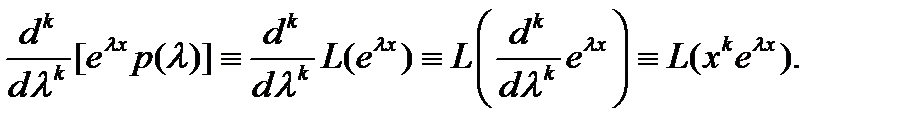
Таким образом, справедливо тождество (8).

Пусть 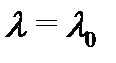– корень кратности 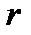характеристического многочлена 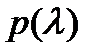уравнения (21.26) с постоянными коэффициентами 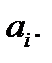Тогда 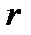функций

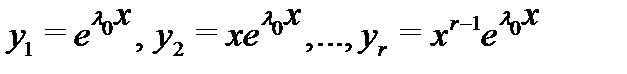
линейно независимы на любом отрезке 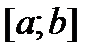и являются решениями уравнения (1).

Доказательство. Пусть 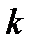–- любое натуральное число, удовлетворяющее неравенству 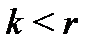. Согласно имеет место тождество

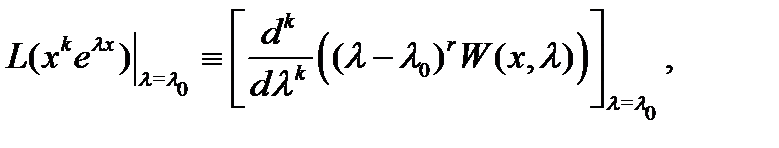
где 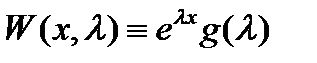(см. 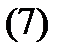). Имеем

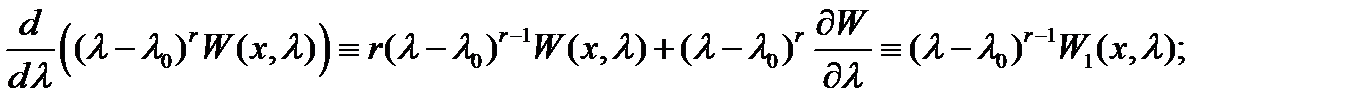
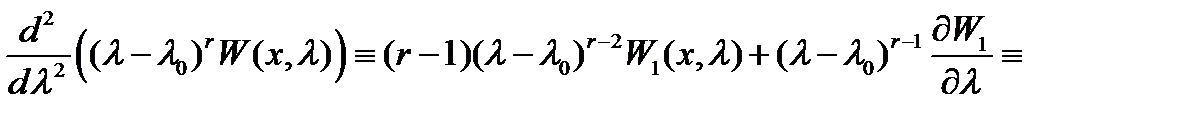
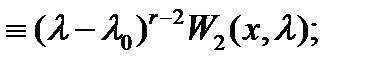
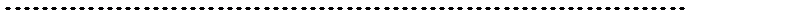
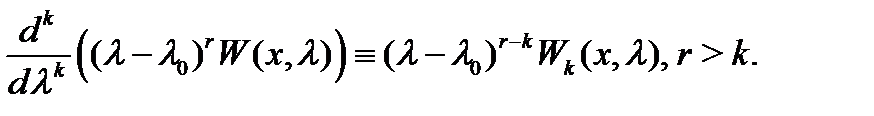
Полагая в последнем тождестве 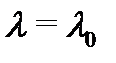, будем иметь

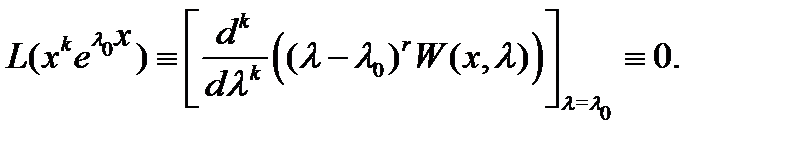
Это означает, что функции (9) являются решениями уравнения (1). Эти функции линейно независимы на любом отрезке 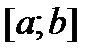(см. утверждение предыдущей лекции). Свойство доказано.

Если 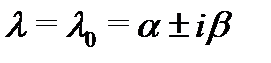– комплексный корень кратности 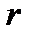уравнения с постоянными и действительными коэффициентами 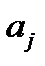, то отделяя в (9) действительные и мнимые части, получаем 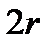линейно независимых действительных решений

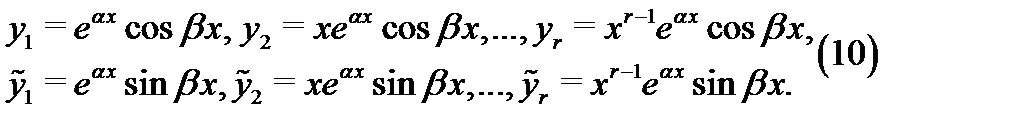
Из этого факта и предыдущих утверждений вытекает следующий алгоритм построения фундаментальной системы решений однородного уравнения (1) с постоянными и действительными коэффициентами .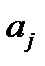

Алгоритм 1.

1) По уравнению (1) составляем характеристическое уравнение , заменив в (1) производные 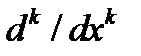на степени ( ).

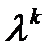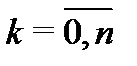2) Найдем корни 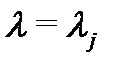характеристического уравнения и установим их кратности.

3) Каждому действительному корню 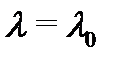кратности поставим в соответствие линейно независимых решений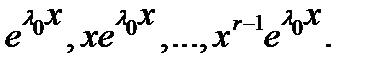

4) Каждой паре комплексно-сопряженных корней 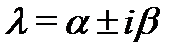кратности 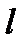сопоставим 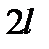линейно независимых решений

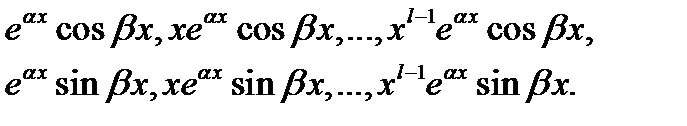
5) Объединим все полученные линейно независимые решения. Получим фундаментальную систему решений уравнения (1), состоящую из 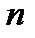функций ( 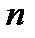– порядок уравнения (1)).

Общее решение уравнения (1) имеет вид

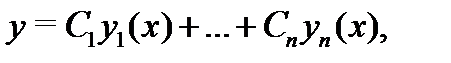
где 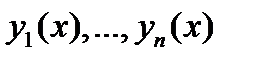– построенная в алгоритме 1 фундаментальная система решений, а 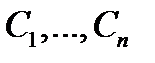–- произвольные постоянные.

Пример 2. Найти общее решение уравнения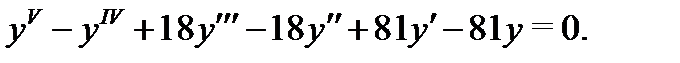

Решение.Составляем характеристическое уравнение , находим его корни и устанавливаем их кратности:

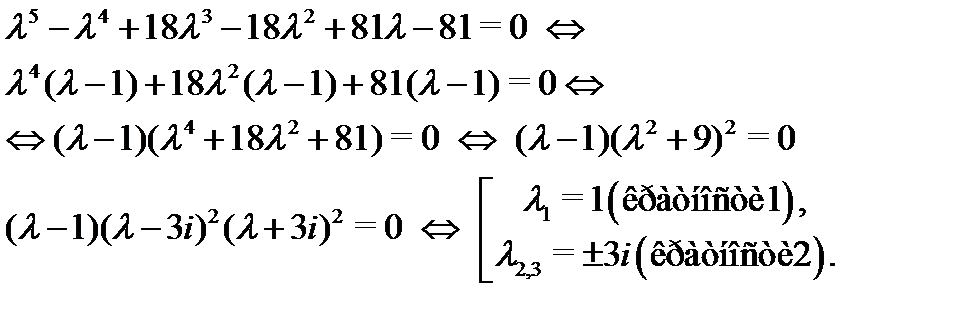
Согласно алгоритму 1 выписываем линейно независимые решения, отвечающие каждому корню:

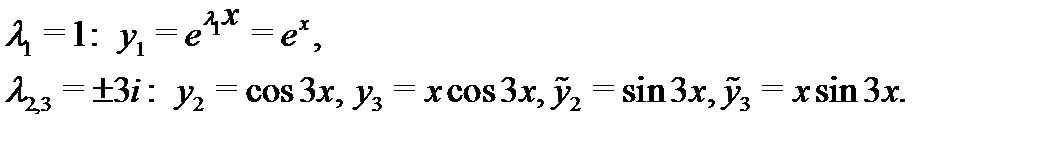
Следовательно, общее решение исходного уравнения имеет вид

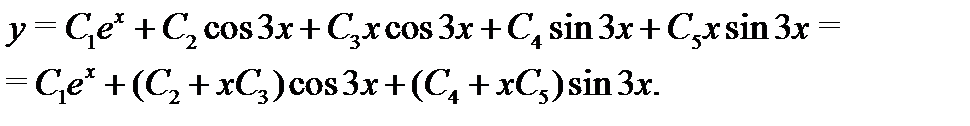
3. Построение общего решения неоднородного уравнения с постоянными коэффициентами. Метод подбора частного решения неоднородного уравнения

Для неоднородного уравнения

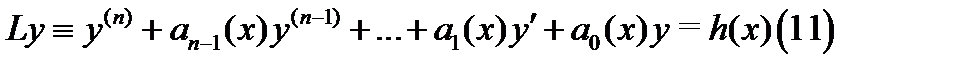
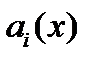с непрерывными на отрезке коэффициентами и неоднородностью 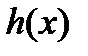был изложен метод вычисления частного решения 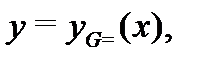называемый методом вариации постоянных. После того как найдено частное решение неоднородного уравнения, его общее решение вычисляется по формул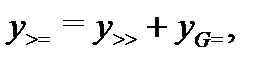е где 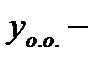общее решение соответствующего однородного уравнения 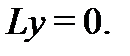Дадим еще один способ вычисления частного решения неоднородного уравнения (11), который применяется и в случае, когда коэффициенты этого уравнения переменные.

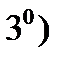Пусть в уравнении (11) все коэффициенты 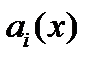и правая часть 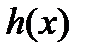непрерывны на отрезке 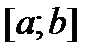и пусть 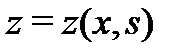– решение соответствующего однородного уравнения 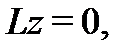удовлетворяющее начальным условиям

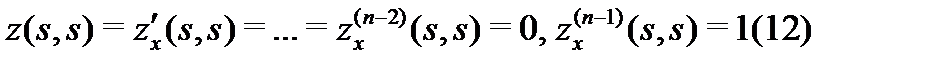
при любом фиксированном значении параметра 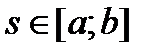. Тогда частное решение неоднородного уравнения (21.22) с нулевыми начальными данными 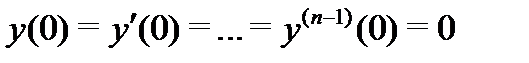может быть записано в виде

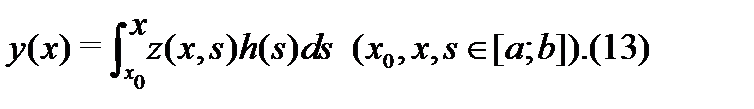
Доказательство. Найдем производные 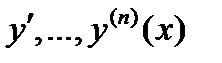функции (13), пользуясь формулой

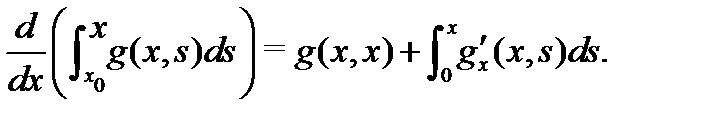
С учетом начальных условий (12), будем иметь

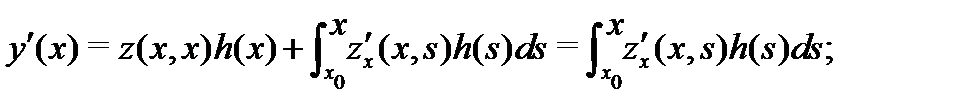
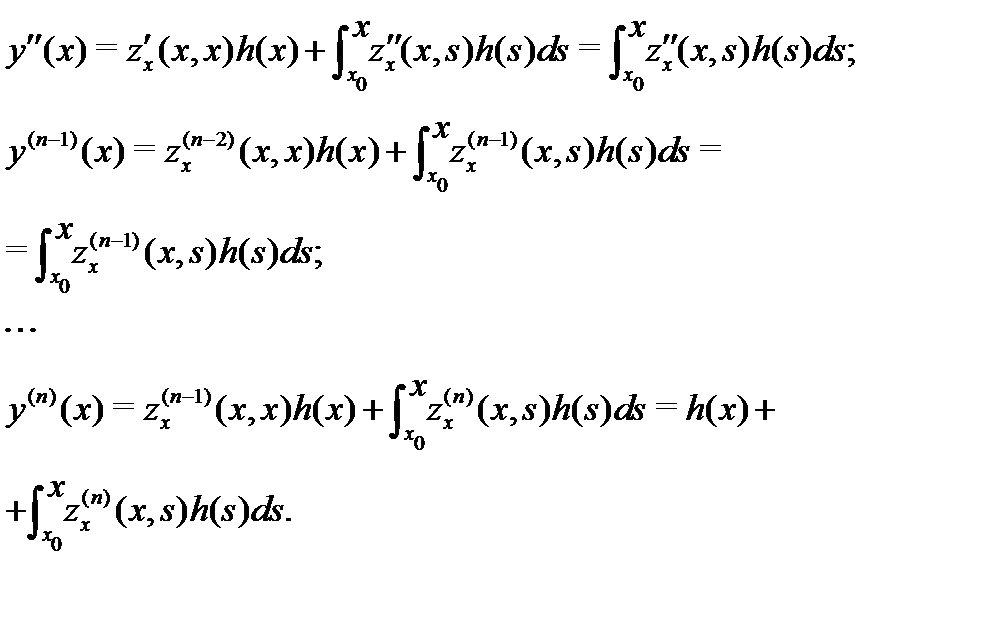
Следовательно,

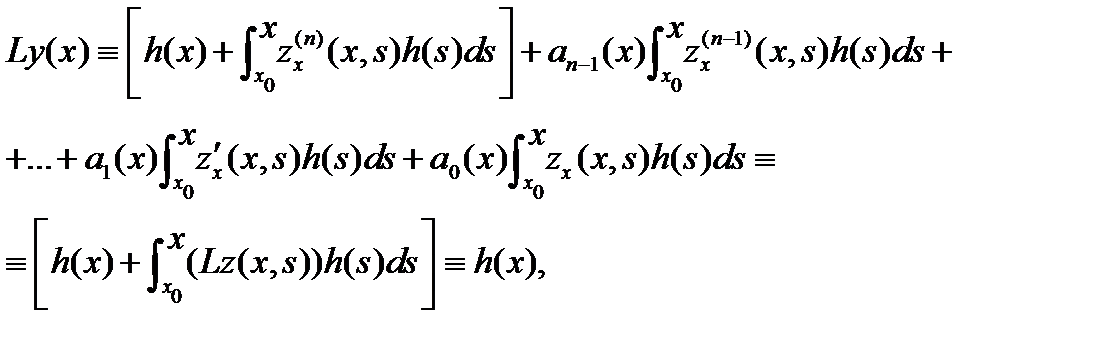
так как 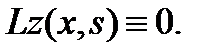Таким образом, функция (13) удовлетворяет неоднородному уравнению 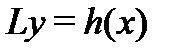. Из выписанных выше равенств для производных функции (13) следует, что она удовлетворяет нулевым начальным условиям. Утверждение доказано.

Пример 3. Найти общее решение неоднородного уравнения

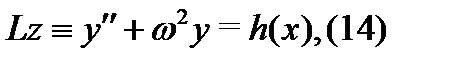
где 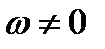– постоянная, а 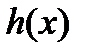–- произвольная непрерывная на отрезке 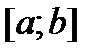функция.

Решение. Построим сначала общее решение соответствующего однородного уравнения 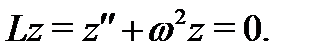Так как его характеристическое уравнение 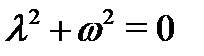имеет два различных комплексно-сопряженных корня 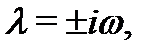то его общее решение имеет вид

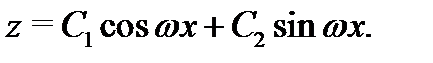
Подчиним это решение начальным условиям

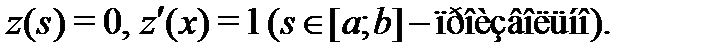
Будем иметь

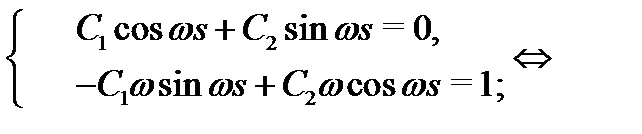
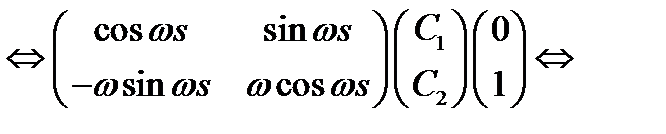
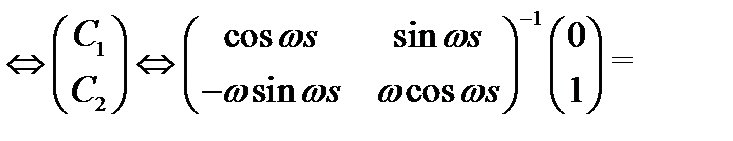
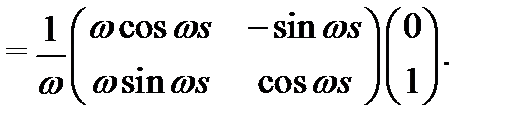
Итак, 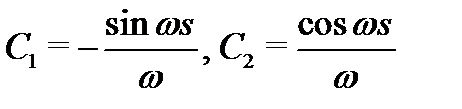, значит

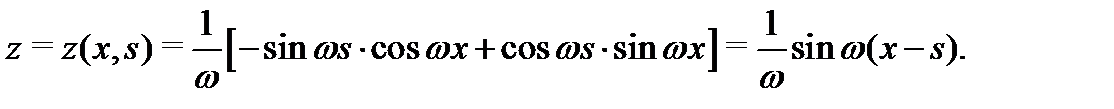
Следовательно, частное решение неоднородного уравнения (14) имеет вид

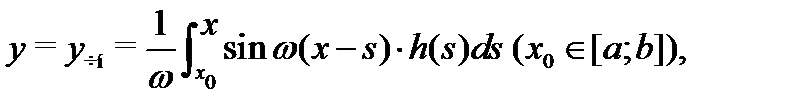
а общее решение этого уравнения запишется в форме

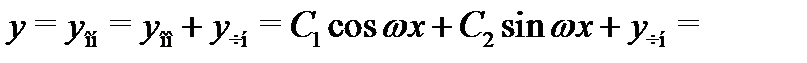
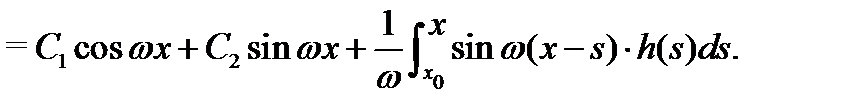
Перейдем теперь к вычислению частного решения неоднородного уравнения (14) с помощью так называемого метода подбора. Оговоримся сразу же, что он применим для уравнений (11) с постоянными коэффициентами и со специальной правой частью вида

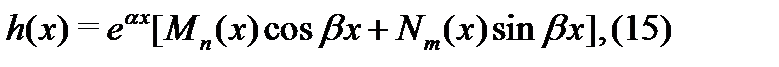
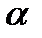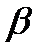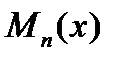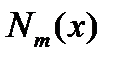где и – постоянные, а и –- многочлены степен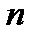и и 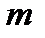соответственно. Заметим, что функции вида

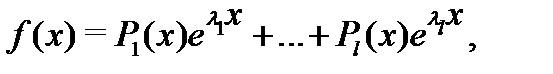
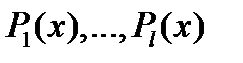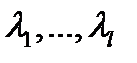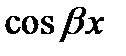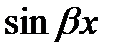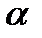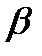где – многочлены, а – постоянные (в общем случае комплексные), называются квазиполиномами (или квазимногочленами). Если выразить в (15) и через экспоненты (см. предыдущую лекцию), то (15) можно представить в виде квазиполинома с комплексными коэффициентами. Поэтому функцию (15) будем также называть квазимногочленом. При этом будем считать, что числа и действительные, а число 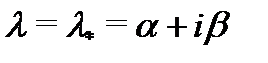будем называть спектральным значением квазиполинома (15). Это число играет важную роль при построении частного решения неоднородного уравнения (11).