Дисперсія для середнього прогнозу

Формула для оцінки дисперсії 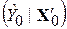має такий вигляд

,

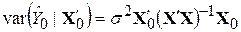(9.9.8)

де 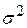– дисперсія залишків 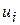, 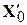– вектор заданих величин Х, у яких ми хочемо отримати прогноз, а 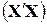– матриця, визначена в (9.3.9), тобто матриця, що застосовується для знаходження коефіцієнтів регресії. Замінюючи 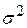на її незміщену оцінку 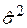, можемо подати (9.9.8) у вигляді

.

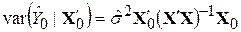(9.9.9)

Для ілюстративного прикладу з розд. 8 отримуємо такі значення:

, .

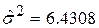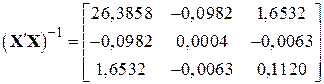Використовуючи ці дані, за формулою (9.9.9) одержуємо

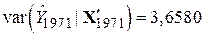
(9.9.10)

і

.

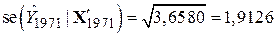(9.9.11)

Тепер, застосовуючи підхід із розд. 5 і 8, можна знайти 100(1–a)%-й довірчий інтервал для середнього прогнозу при заданому Х₀:

.

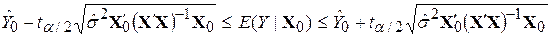(9.9.12)

Дисперсія для індивідуального прогнозу

Формула для обчислення дисперсії для індивідуального прогнозу має такий вигляд:

,

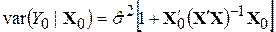(9.9.13)

де .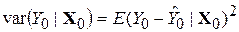

Використовуючи наші дані, одержуємо

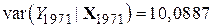
(9.9.14)

і

.

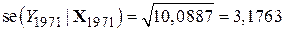(9.9.15)

Якщо ми хочемо визначити 100(1–a)%-й довірчий інтервал для індивідуального прогнозу, то можемо застосувати формулу (9.9.12), у якій стандартна похибка прогнозу визначається з (9.9.13). Очевидно, що стандартна похибка для індивідуального прогнозу більша, ніж для середнього.