Матричне формулювання ANOVA-таблиці

для лінійної моделі регресії з k змінними.

Джерело дисперсії	SS	DF	MSS
Унаслідок регресії		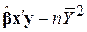k–1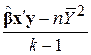
Унаслідок залишків		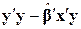n–k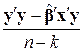
Загальна		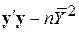n–1

Припускаючи, що збурення розподілені нормально й нульова гіпотеза є 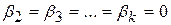, як і в розд. 8, можна показати, що

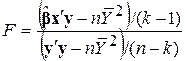(9.7.1)

розподілено за законом F-розподілуз (k–1) і (n–k) степенями вільності.

У розд. 8 ми бачили, що при зроблених вище припущеннях існує тісний зв’язок між F і R², а саме

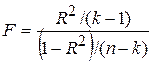Отже, табл. 9.2 може бути перетворена до вигляду табл. 9.3.

Таблиця 9.3

ANOVA-таблиця для k змінних в термінах R²

Джерело дисперсії	SS	DF	MSS
Унаслідок регресії		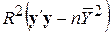k–1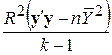
За залишками		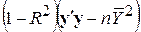n–k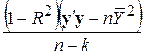
Загальна		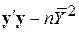n–1

Однією з переваг табл. 9.3 в порівнянні з табл. 9.2 є те, що весь аналіз може бути виконаний у термінах R²; немає потреби розглядати складова 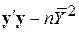, оскільки він випадає з виразу для F.

9.8. Перевірка лінійних обмежень. ЗагальнийF-тест у матричних позначеннях

У розд. 8 ми описали загальний F-тестдля перевірки справедливості лінійних обмежень, що накладаються на один або більше параметрів лінійної регресії з k змінними. Відповідний тест визначається рівнянням (7.4.9). Матричний аналог цього рівняння можна отримати дуже легко. Хай

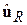- – вектор залишків регресії з обмеженнями;

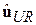- – вектор залишків регресії без обмежень.

Тоді

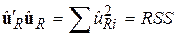- з регресії з обмеженнями;

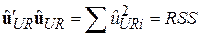- з регресії без урахування обмежень;

- m – кількість лінійних обмежень;

- k– кількість параметрів у регресії без обмежень;

- n – кількість спостережень.

Матричний аналог формули (7.4.9) має вигляд

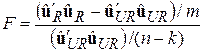(9.8.1)

У цій формулі F підкоряється закону F-розподілуз (m, n–k) степенями вільності. Як завжди, якщо підрахована величина F більша критичного значення, ми можемо відкинути обмеження на регресію, у протилежному випадку ми їх не відкидаємо.