Залишкова дисперсія

.

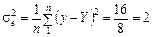У невеликих за обсягом сукупностях коефіцієнт регресії схильний до випадкових коливань. Тому слід перевірити його істотність. Коли зв’язок лінійний, істотність коефіцієнта регресії перевіряють за допомогою t-критерію (Стьюдента), статистична характеристика якого для гіпотези 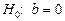визначається відношенням коефіцієнта регресії b до власної стандартної похибки 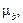тобто .

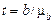Стандартна похибка коефіцієнта регресії залежить від варіації факторної ознаки 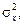залишкової дисперсії 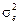і числа ступенів свободи 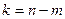, де m — кількість параметрів рівняння регресії:

.

Для лінійної функції m = 2. За даними табл. 7.3 маємо:

.

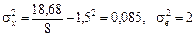Звідси 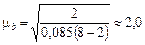(ц/га), а 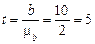, що перевищує критичне значення двостороннього t-критерію 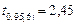(табл. 6.3). Гіпотеза про випадковий характер коефіцієнта регресії відхиляється, а отже, з імовірністю 0,95 вплив кількості внесених добрив на врожайність зернових визнається істотним.

Для коефіцієнта регресії, як і для будь-якої іншої випадкової величини, визначаються довірчі межі 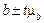. У нашому прикладі довірчі межі коефіцієнта регресії з імовірністю 0,95 (t = 2,45) становлять .

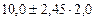Важливою характеристикою регресійної моделі є відносний ефект впливу фактора х на результат у — коефіцієнт еластичності:

.

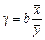Він показує, на скільки процентів у середньому змінюється результат у зі зміною фактора х на 1%. У нашому прикладі 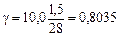тобто збільшення кількості внесених добрив на 1% спричинює приріст урожайності зернових у середньому на 0,8%.

Оцінити відносний ефект впливу фактора х на результат у можна безпосередньо на основі степеневої функції Y = ax^b, параметр b якої є коефіцієнтом еластичності. Степенева функція зводиться до лінійного виду логарифмуванням lg Y = lg a + b lg x. До класу степеневих належать функції споживання, виробничі функції тощо.