Отже, наприклад, змінна

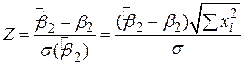
(3.2.1)

є стандартизована нормальна змінна. Якщо 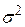відома, то важливою властивістю нормально розподіленої величини зі сподіванням 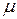і дисперсією 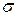є те, що площа під густиною розподілу між 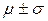становить 68%, між 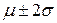– близько 95%, а між 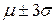– близько 99,7%.

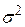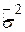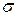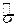На практиці відома рідко і замінюється її незміщеною оцінкою . Якщо замінити в (3.2.1) на , то можна отримати

, ,

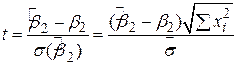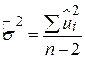(3.2.2)

де 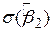- стандартна помилка оцінювача 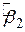. Можна показати, що визначена таким чином змінна t розподілена за законом розподілу Ст’юдента з N–2 степенями вільності. Слід звернути увагу на різницю між (3.2.1) і (3.2.2). Отже, замість того щоб застосовувати нормальний розподіл, ми можемо застосовувати розподіл Ст’юдента для побудови довірчого інтервалу величини :

,

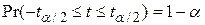(3.2.3)

де t визначається за формулою (3.2.2), а 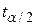є величиною розподілу Ст’юдента для 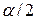рівня значимості і N–2 степеня вільності. Вона часто називається критичною величиною при 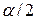рівні значимості. Підстановка (3.2.2) у (3.2.3) дає рівність

.

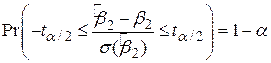(3.2.4)

Перетворюючи (3.2.4), одержуємо

.

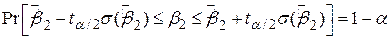(3.2.5)

Ця рівність являє собою 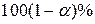-й довірчий інтервал для , який може бути записаний більш компактно у вигляді

.

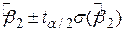(3.2.6)

За аналогією з цим, застосовуючи (3.2.1) і (3.2.2), ми можемо записати довірчий інтервал для :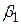

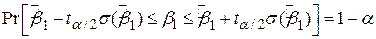
(3.2.7)

або більш компактно

.

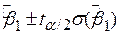(3.2.8)

Відзначимо важливу межу довірчих інтервалів (3.2.6) і (3.2.8). В обох випадках довжина довірчого інтервалу пропорційна стандартній помилці оцінювачів. Тобто чим більша стандартна помилка, тим більша довжина довірчого інтервалу. Інакше кажучи, чим більша стандартна помилка оцінювача, тим більша невизначеність оцінки істинного значення параметра. Так, стандартна помилка оцінювача часто описується як міра точності оцінювача, тобто наскільки точно оцінювач вимірює дійсний параметр генеральної сукупності.

Повертаючись до нашого ілюстрованого прикладу моделі “споживання-дохід”, нагадаємо, що ми знайшли 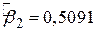, 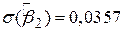і df=8. Якщо ми покладемо 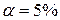, тобто 95%-й довірчий коефіцієнт, тоді за таблицею розподілу Ст’юдента знаходимо критичне 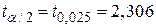. Підставляючи цю величину в (3.2.5), можна перевірити, що 95%-й довірчий інтервал для 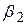буде

.

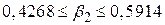(3.2.9)

Або, застосовуючи (3.2.6),

,

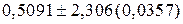тобто

.

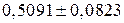(3.2.10)

Інтерпретація цього довірчого інтервалу така: для даного 95%-го довірчого коефіцієнта при довготривалій вибірці в 95 зі 100 випадків інтервали типу (0,4268; 0,5914) міститимуть істинне . Але, як ми попереджали раніше, зауважимо, що не можна говорити про імовірність у 95% того, що специфічний інтервал (0,4268; 0,5914) містить істинне , оскільки цей інтервал фіксований; отже, або лежить у ньому, або ні. Таким чином, імовірність знаходження у фіксованому інтервалі дорівнює або 1, або 0.

Згідно з (3.2.7) можна перевірити, що 95%-й довірчий інтервал для 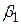в нашому прикладі буде

,

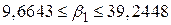(3.2.11)

або, використовуючи (3.2.8), ми знаходимо

,

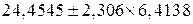тобто

.

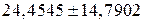(3.2.12)

Ще раз нагадаємо про правильну інтерпретацію цього довірчого інтервалу.

3.3. Довірчий інтервал для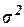

Як було зазначено в розд. 2, при припущенні про нормальність розподілу 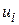змінна

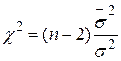
(3.3.1)

розподіляється за законом розподілу з (N–2) степенями вільності. Отже, для побудови довірчого інтервалу для змінної 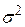ми можемо застосовувати закон розподілу

,

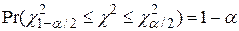(3.3.2)

де - визначена за формулою (3.3.1) змінна, що стоїть посередині нерівності, а 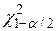і 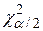- дві величини (критичні величини ), отримані з таблиць розподілу згідно із законом з (N–2) степенями вільності, причому такими, що відсікають 100(a/2)% хвостових областей розподілу , як показано на рис. 3.1.

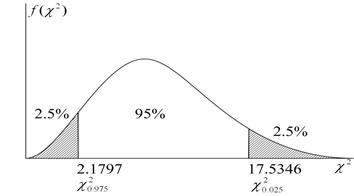
Рис. 3.1. 95%-й довірчий інтервал для розподілу з df = 8

Підставляючи в (3.3.2) з рівності (3.3.1) і перерозподіляючи члени, одержуємо

,

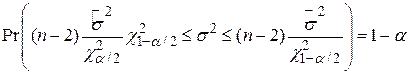(3.3.3)

який дає 100(1–а)%-й довірчий інтервал для .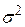

Як ілюстрацію розглянемо досліджений раніше приклад (2.6.1)-(2.6.2):

, , , , , , , , , , , .

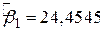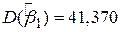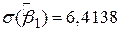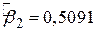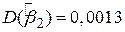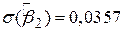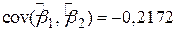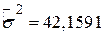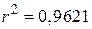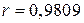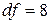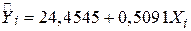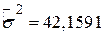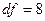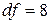Тут ми маємо і . Якщо вибрати a=5%, то таблиця розподілу для дає такі критичні величини: 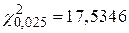і 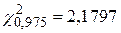. Вони показують, що імовірність величини бути не менше 17,5346 складає 2,5% і не перевищувати 2,1797 є 97,5%. Отже, обмежений цими двома значеннями інтервал є 95%-й довірчий інтервал для , як показано на рис. 3.1.

Підставляючи дані нашого прикладу в (3.3.3), можна перевірити справедливість такого 95%-го довірчого інтервалу для :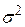

, .

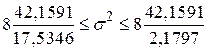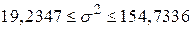Інтерпретація цього інтервалу така: якщо ми встановимо 95%-ві довірчі межі і будемо повторювати багато разів цю процедуру, то в 95 випадках зі ста лежатиме всередині цих інтервалів.