Этапы моделирования

Этапы моделирования показаны на блок-схеме рис.3.

На схеме видны многочисленные обратные связи — возвращение к предыдущим этапам после анализа промежуточных и конечных результатов моделирования. Это характерно для прикладных исследований. В процессе эксперимента уточняются постановка задачи, её формализация, допущения, совершенствуются вычислительные алгоритмы.

Рис. 3

При моделировании сложной системы часто оказывается удобным, а порой и необходимым, провести декомпозицию — разделение системы на модули, после чего модель сложной системы будет состоять из связанных между собой моделей этих модулей. Структура полученной таким образом сложной модели должна соответствовать структуре и иерархии исходной системы, точнее, полученная модель должна быть адекватна исходной модели в том смысле, как это определено выше.

Соответственно, создание модели сложной системы включает две дополнительные операции: (1) декомпозицию системы, деление её на модули и (2) согласование отдельных модулей, их входов и выходов.

Для моделей сложных систем характерно, что:

- одна и та же информация оказывается необходимой для разных блоков — моделей модулей системы;

- при совместной работе блоков сложной модели требуется видоизменение информации при передаче её от одного блока к другому (т.е. интерфейсная адаптация). В связи с этим при моделировании сложной системы особое внимание уделяется способам хранения информации и организации информационных потоков.

Декомпозицию и согласование при создании модели сложной системы следует отнести к этапу 2 (рис. 3).

Достоинство математики — применение одинаковых моделей для изучения различных по физической природе и решаемым задачам системам. Это не противоречит утверждению, что для решения каждой конкретной проблемы нужна своя индивидуальная модель.

Как бы ни была сложна и «индивидуальна» модель, всегда при её создании используются разработанные ранее для других целей блоки моделей и методы, а также накопленный методический опыт.

3.6. Значение и содержание этапа «Постановка задачи»

Постановка задачи является 1-м этапом моделирования. Решающее значение этого этапа для успеха исследования отмечается во всех работах, посвященных методологии моделирования.

Сформулировать задачу на языке математики — это значит более чем наполовину решить её. /8/ Ошибка в постановке задачи может однозначно определить неудачу дальнейших исследований. Как писал Валерий Брюсов: «Однажды ошибясь при выборе дороги, / шли вдаль ученые, глядя на свой компас. / И был их труд высок, шаги их были строги, / но уводил их прочь от цели каждый час».

Правильное формулирование задачи — это научная проблема не менее сложная, чем решение задачи, и не нужно надеяться, что кто-то другой сделает это за вас». /3/

Проблема постановки задачи возникает зачастую, как состояние неудовлетворенности. Ситуация становится проблемной, когда действие какой либо системы, течение какого либо процесса не приводят к желаемому результату.

Известна следующая оценка времени на отдельные этапы моделирования:

- постановка задачи — 40-50%;

- разработка модели — 20-30%;

- эксперимент, анализ результатов — 20-30%.

При постановке задачи решаются следующие взаимосвязанные задачи.

1) Уяснение цели (задачи) исследования.

2) Изучение объекта моделирования (системы, процесса).

3) Анализ доступной информации.

4) Выявление релевантных факторов.

5) Формулирование альтернатив.

6) Определение ограничений и допущений. Определение диапазона изменения параметров и переменных.

7) Выбор критерия, системы критериев качества достижения цели.

8) Установление масштаба предстоящего эксперимента.

9) Математическая постановка (формулировка) задачи.

Вследствие взаимосвязанности перечисленных задач, строгой последовательности их решения не существует. Так, уяснить задачи исследования и грамотно даже на доматематическом уровне сформулировать эти задачи возможно только после определенного уровня ознакомления с объектом; изучение объекта продолжается в течение всего этапа постановки задачи; например, после анализа доступной информации может последовать определенная корректировка задачи исследования.

В приведенном перечислении этапов постановки задачи предполагается, что система существует, и в процессе прикладного исследования могут исследоваться характеристики системы, разрабатываться рекомендации по изменению ее параметров, вырабатываться рекомендации по управлению системой, решаться и некоторые другие задачи. Существенно сложнее обстоит дело, когда создается новая система. В таком случае на этапе 2 необходимо уяснить цели создания системы, задачи, которые она должна решать, предполагаемое ее взаимодействие с внешней средой и с другими системами и еще многие обстоятельства, обеспечивающие в дальнейшем существование системы. Только после этого можно вернуться к этапу 1 уяснению задач прикладного исследования.

Далее приводятся краткие пояснения существа перечисленных задач.

(1).Без четкой формулировки на вербальном уровне задач исследования дальнейшая работа может оказаться просто бессмысленной, и выбор лучшего решения окажется лишь математическим упражнением.

Здесь еще раз уместно подчеркнуть, что любое серьезное исследование начинается с изучения системы, ее целей, структуры, взаимодействия с окружающей средой, перспектив существования и развития. Только после этого можно четко понять задачи исследования. Формирование задачи заказчиком, если таковой имеется, следует рассматривать лишь как первое приближение. При рассмотрении требующей решения задачи одновременно с уяснением ее сущности происходит и «расширение» задачи. Например, в социально-экономических системах очень важно уточнить круг лиц, заинтересованных в достижении системой определенного состояния или настроенных к этому отрицательно, а быть может, и враждебно. К сожалению, недооценка изложенных положений явление нередкое.

(2). Характер изучения системы решающим образом зависит от следующих обстоятельств: физической природы системы, ее целей и задачи (цели) исследования. При изучении системы необходимо понять ее назначение, структуру, границы, взаимодействие с окружающей средой, перспективы существования и развития. В общем случае цель системы заключается в достижении наиболее эффективным (оптимальном) способом желаемого, наилучшего, в каком то смысле, состояния с учетом реальных ограничений. Предполагается, что цель системы («желаемое» состояние системы) известна. Но как раз это зачастую либо совсем не ясно, либо сформулировано в общем виде и без понимания, что не все желаемое достижимо Особое внимание следует уделять отношениям, реально существующим между элементами системы, сути существующих в системе проблем и причин, вызвавших эти проблемы.

Проблема возникает, как ощущение неудовлетворенности состоянием системы. Существо проблемы, зачастую, отчетливо не осознается. Причинами неудовлетворенности могут быть внутрисистемные трудности на пути достижения цели или изменение внешних условий, следствием которых оказывается необходимость изменения целей или корректировки траектории движения к цели.

Проблемы могут быть простыми, выяснение причин которых не требует специальных исследований, сложными — уяснение их причин связано со специальными исследованиями, и очень сложными, возможно потребующими изменение фундаментальных концепций системы или разработки принципиально нового методического аппарата для уяснения причин проблемы. В общем случае для понимания сути проблемы, ее формулировки на доматематическом уровне и выявления причин возникновения проблемы требуются значительные усилия.

При возникновении проблем естественно возникает вопрос, была ли эта проблема известна ранее, если «да», то принимались ли в связи с этим какие либо решения Возможны следующие варианты:

- проблема новая, ранее не известная;

- проблема была известна ранее, но решение не принималось, или решение принималось, но было неверным, или решение было верным, но было не выполнено.

В зависимости от варианта ответа предпринимаются действия по уяснению проблемы, выработки решения и обеспечению выполнения решения.

Проблема может быть выявлена руководителем или любым сотрудником организации. В сложных системах (организациях) целесообразно иметь специальную группу сотрудников для выявления отклонений реального состояния системы от желаемого. Важно улавливать симптомы причин, могущих вызвать проблему, своевременно реагировать на них, не дожидаясь, когда причины породят проблему. Если проблема возникла, необходимо не только разрешить проблему, но и устранить причины, которые ее вызвали. При уяснении проблемы должны быть раскрыты все неопределенности, выявлены релевантные причины, исключены из рассмотрения причины второстепенные. При возможности должны быть собраны количественные данные относительно параметров рассогласования реального и желаемого состояний системы, а также параметров, характеризующих причины проблемы.

Удобным инструментом для углубленного понимания проблемы, анализа причинно-следственных отношений, выявления возможных последствий изменения этих отношений является когнитивная структуризация — новое направление системного анализа. Цель когнитивной структуризации в формировании и уточнении исследуемого объекта (оргсистемы), рассматриваемого как сложная система, состоящая из отдельных элементов — подсистем.

Для анализа сложной системы строится структурная схема причинно-следственных связей, называемая когнитивной картой и являющаяся знаковым ориентированным графом. Два элемента А и В,изображаются в виде вершин графа, соединенных ориентированной дугой: А ® В.Здесь А —причина, В —следствие. Причинно-следственные связи (отношения) разделены на два типа:

- положительные, если увеличение (усиление) А ведет к увеличению (усилению) В, а уменьшение А ведет к уменьшению В;

- отрицательные, если увеличение А ведет к уменьшению В, а уменьшение А — к увеличению В.

Положительная связь помечается на схеме знаком «плюс» над дугой, отрицательная — знаком «минус».

Количественная оценка отношений в сложных системах трудоемка. Требуется привлечение экспертов, анкетирование с последующей статистической обработкой данных и пр. Однако нередко оказывается возможным получить содержательные выводы с помощью только качественных оценок, основанных на опыте и интуиции исследователя.

Исследователи зачастую чрезмерно упрощают ситуацию из-за трудностей учета большого числа факторов, их сложного динамического взаимодействия. Причиной необоснованных упрощений могут быть и недостаток опыта или знаний у исследователя. Только немногие общественные явления зависят от одной причины. Обычно общественные явления включают много различных событий, тенденций, определяемых взаимосвязанными факторами. Образуется сеть причинных ограничений, т.е. причинность носит системный характер.

Приобретение опыта построения и анализа когнитивных карт избавит исследователя от ошибок свойственных несистемному мышлению, научит пониманию, что событие может иметь множество причин. Это, в свою очередь, позволит более полно разбираться в сложных проблемах, принимать обоснованные решения.

Использование когнитивных карт в организациях для анализа проблем и планирования может быть связано с анализом нескольких тысяч причинно-следственных связей. Соответственно потребуется привлечение ЭВМ и специально разработанного программного обеспечения.

(3). Информация нужна не любая, а только та, которая действительно обеспечит решение задачи. Излишние подробности могут только помешать решению задачи. «Информацию нужно профильтровать, отделить важное от неважного, нужное от ненужного, а отсеянное нужно представить в наиболее выразительной легко усвояемой форме. И это тоже задача прикладной математики, которой на этот раз приходится работать на грани психологии и социологии». Необходимо также получить надежные оценки точностных характеристик исходной информации. «Для успеха исследования настолько важно иметь беспристрастные, независимые от субъективных оценок фактические данные, что все они должны быть проверены и перепроверены независимо от того, из какого источника они
получены».

Типичной ошибкой является начало исследований со сбора информации, т.е. до того, как уяснена постановка задачи и намечена, хотя бы в первом приближении, методика исследования. Если информация собиралась до выяснения перечисленных обстоятельств, то велика вероятность, что будет собрано много ненужной информации, а что-нибудь очень необходимое отсутствует. Важно также учитывать фактор старения
информации.

Характеристики доступной информации (полнота, достоверность, точность) влияют на структуру модели, методику проведения эксперимента. Недооценка этих обстоятельств приводит к появлению моделей, называемых информационно уродливыми.

(4). Релевантными называются факторы, существенным, решающим образом влияющие на результаты исследования. После определения релевантных факторов производится выбор тех из них, которые могут быть описаны количественно, уточнение списка этих факторов путем объединения их по общим признакам и исключения существенно коррелированных факторов. После уточнения списка релевантных факторов потребуется убедиться, не приведет ли отказ от некоторых факторов к недопустимому снижению точности решения задачи или, что существует такая вероятность. При внимательном рассмотрении может выясниться, что некоторые факторы, отнесенные вначале к неизмеримым, могут быть оценены косвенно.

(5). На начальном этапе необходимо сохранить все возможные, в том числе кажущиеся нелепыми альтернативы решения задачи. Пренебрежение «нелепыми» альтернативами, поспешность в их отбрасывании, уступка соблазну поскорее начать вычисления, «развернуть работу» и ухватиться за первую показавшуюся хорошей альтернативу, может обернуться потерей действительно хорошего решения. В простейшем случае вместо выбора альтернатив требуется определить диапазоны изменения переменных и параметров модели.

Существует несколько организационных форм генерирования
альтернатив.

а) Мозговой штурм. Формируется группа специалистов, состав которой зависит от характера проблемы и вида системы. Члены группы высказывают различные альтернативы решения проблемы, которые фиксируются, причем на этом этапе критика выдвигаемых альтернатив запрещена. Обращается внимание на взаимосвязь альтернатив, возникновение новых идей как развитие ранее выдвинутых предложений.

б) Синектика — генерирование идей путем ассоциативного мышления. Среди задач, решение которых известно, находятся аналоги исследуемой проблеме. Например, в /17/ задача столкновения двух вражеских группировок решена на основе аналога — процесса взаимного проникновения молекул двух соприкасающихся химических веществ.

в) Разработка сценариев. Проводится описание будущего течения процесса при различных альтернативах, но при одинаковых начальных условиях. При этом важно учесть все релевантные факторы, влияющие на процесс.

г) Морфологический анализ. Определяются все возможные значения основных переменных и рассматриваются все возможные комбинации значений этих переменных. Например, при выборе вида проектируемого телевизора переменными являются цвет (черно-белый, двухцветный,..., семицветный), размер изображения, градации яркости, и пр. Всего возможно более 300 комбинаций переменных. Безусловно, при рассмотрении комбинаций некоторые варианты могут быть отброшены, как не удовлетворяющие очевидным требованиям.

д) Деловые игры. Создаются имитационные человеко-машинные системы для анализа течения процессов при различных решениях участников игры — лиц, которым надлежит принимать решения в реальной ситуации.

(6). Отказ от факторов, отнесенных к нерелевантным, сознательное упрощение ряда зависимостей, ограничение области изменения некоторых переменных и пр. способствуют упрощению модели, удешевлению эксперимента. Однако при упрощении модели может быть потеряна адекватность модели. Поэтому при постановке задачи необходимо составить список принятых допущений с тем, чтобы вернуться к нему при анализе результатов моделирования. Не исключено, что на полученные результаты сильное влияние оказали неоправданные допущения и необходимо вернуться к уточнению постановки задачи.

(7). Критериальная (целевая функция) — это отражение целей исследования и правило (алгоритм) оценки этой цели. Критерии должны обеспечить наилучшее, в определенном смысле, решение. В общем случае проблема выбора критерия — это установление признака, по которому определяется предпочтительность. В явном виде критерий может быть и не сформулирован, но характер, вид предпочтительности определен. Задача упрощается, если удается ограничиться одним критерием, но для реальных задач более свойственна многокритериальность — т.е. векторный критерий.

Примеры задач, в которых используется векторный критерий.

(а) Задачи оптимизации на множестве целей, каждая из которых должна быть учтена при выборе лучшего решения (альтернативы).

(б) Задачи оптимизации на множестве объектов (подсистем). Качество функционирования каждой подсистемы оценивается своим, частным критерием, а системы в целом — некоторым общим, векторным критерием, составленным из частных критериев.

(в) Задачи оптимизации на множестве условий (или временных этапов). Качество функционирования для каждого условия (этапа) оценивается частным критерием, а для всех условий (этапов) — векторным критерием, составленным из частных.

(г) Многоуровневые векторные задачи оптимизации, в которых компоненты векторного критерия являются не скалярами, а более сложными образованьями.

К векторным критериям предъявляются следующие дополнительные требования:

- полнота, ввод дополнительных критериев не должен повлиять на результаты решения;

- минимальность, набор частных критериев должен быть наименьшим из всех возможных наборов, обеспечивающих оптимальный выбор.

Частный критерий k_j(x), (xÎX, X — множество альтернатив) выбирается так, что бы по мере улучшения решения (приближения к заданной цели) критерий монотонно увеличивался или уменьшался. Далее будем полагать, что для всех частных критериев предпочтительным является увеличение значения критерия. Чтобы воспользоваться таким предположением, достаточно изменить знак у тех критериев, уменьшение которых соответствует лучшему решению.

В простейшем случае для многокритериальных задач правило достижения лучшего решения — принцип оптимальности можно сформулировать по аналогии с однокритериальными задачами следующим образом. Оптимальное решение задачи с векторным критерием K ={k_j(x)} jÎ(1,2,...,n) достигается, если все частные критерии k_j(x) достигают максимума одновременно, т.е. существует такая альтернатива x^* что k_j(x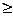^*) k_j(x) для всех x Î X и jÎ(1,2,...,n).,причем хотя бы для одного частного критерия имеет место строгое неравенство.

Однако подобная ситуация для реальных задач не типична. Обычно увеличение одних критериев сопровождается уменьшением других. В подобных случаях оказывается необходимым прибегнуть к некоторому компромиссу и сформулировать принцип оптимальности в следующем виде: Лучшей альтернативой (оптимальным решением) считается такая альтернатива, на которой, хотя и не обеспечивается максимальное значение каждого критерия, но при привлечении дополнительных соображений, в том числе об относительной приоритетности частных критериев, обеспечивается в каком-то смысле лучшее значение векторного критерия.

Таким образом, задачу с векторным критерием можно сформулировать следующим образом: требуется найти альтернативу x^* (оптимальное решение x^*), удовлетворяющее двум условиям:

(1). x^* Î X, где X — множество всех возможных альтернатив;

(2). x^* — наилучшее решение согласно принципу оптимальности, учитывающему принятую схему компромисса между частными целями.

Задачи поиска лучшего решения для трех распространенных схем компромисса можно сформулировать следующим образом.

Схема 1. Ищется альтернатива, доставляющая максимум одному, наиболее предпочтительному критерию при условии, что значения остальных критериев будут не менее некоторых заданных заранее величин — c_j.

k₁(x) ® max; xÎX; k_j(x) ³ c_j; j= ,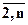

здесь k₁(x)-наиболее предпочтительный критерий,

c_j- заданное минимально допустимое значение j-го критерия.

Схема 2. Ищется альтернатива xÎX,накоторой достигается максимум минимального частного критерия.

.

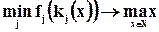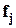— функции, нормализующие критерии, т.е. приводящие их к единой размерности и масштабу. Нормализация необходима, если частные критерии имеют различный физический смысл и измеряются в различных единицах.

Схема 3. Строится обобщенная функция частных критериев

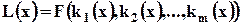
и ищется альтернатива, доставляющая максимум этой функции. Распространенной, но не обязательно лучшей, в конкретной задаче, является функция свертки вида:

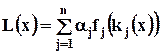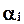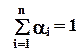, >0, , где:

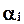— коэффициенты, учитывающие приоритетность частных критериев.

Здесь приведены схемы поиска решений. Алгоритм реализации этих схем должен учитывать особенности конкретной задачи и определенные условия возможности применения схемы. Так, например, в 1 необходимо вначале построить множество Парето, свертка 4 может быть использована в специально оговоренных условиях.

Часто в критерий закладывается одновременно оценки качества решения задачи и какой ценой это качество достигается (критерии вида эффективность-стоимость). Критерии должны быть, по возможности, не чувствительны к небольшим ошибкам во входной информации.

Вследствие сложности реальных задач иногда приходится прибегать к приближенным критериям, которые зачастую дают хороший результат.

Очевидно, что от вида критерия может существенно зависеть оценка относительной ценности альтернатив. Рекомендуется проводить сравнение результатов, полученных при различных критериях.

(8). Окончательное определение масштаба эксперимента производится на этапе «Планирование эксперимента». Однако уже при постановке задачи необходимо оценить предполагаемый масштаб эксперимента и, в том числе, ограничения, которые могут возникнуть в связи с недостатком ресурсов и средств. Последние ограничения достаточно типичны для прикладных исследований и, соответственно, влияют на вид создаваемой модели. При разработке модели учитывается и предполагаемый характер использования модели — будет ли модель использоваться неоднократно.