Классификация моделей

Существует много классификаций моделей, характеризующих свойства моделей, особенности их применения, происхождение. Понимание классификаций моделей является одним из условий их грамотного применения. При этом оказываются полезными ответить на следующие вопросы.

Какого вида (типа) модель более всего подходит для решения поставленной задачи? К какому классу относится разрабатываемая модель и в чём особенности её использования?

Приведём некоторые основные классификации.

1) В зависимости от особенностей возникновения модели могут быть разделены на три группы:

а) феноменологические, возникающие в результате наблюдения объекта, явления, его осмысливания;

б) асимптотические — их появление результат дедукции. Новая модель появляется как частный случай более общей модели. Переход от феноменологических моделей к асимптотическим характеризует определённую зрелость науки;

в) модели ансамблей — возникли в результате процесса индукции. Новая модель является обобщением или синтезом отдельных моделей. В моделях ансамблей свойство отдельных объектов исследуются с учётом взаимодействия объектов. Модели ансамблей не могут быть получены путем механического объединения моделей отдельных объектов в модель системы. При объединении объектов в систему внутренние свойства объектов могут изменяться, что особенно заметно при изучении социально-экономических систем.

2) В зависимости от способа описания свойств моделируемого объекта различают модели вербальные, изобразительные, аналоговые, символические.

Вербальные — это словесные, описательные модели.

В изобразительных моделях изучаемые свойства (отношения) объекта представлены этими же свойствами (отношениями), но, как правило, в другом масштабе. Например, модель самолёта для продувки в аэродинамической трубе, модель солнечной системы в планетарии, модель гидроузла в конструкторской организации.

В аналоговых моделях свойства объекта отображаются набором специфических свойств модели. Так, при аналоговом моделировании полёта самолёта параметры (координаты, скорость) самолёта отображаются в модели значениями напряжения, силы тока. Другой пример, множество точек земной поверхности с одинаковой высотой над уровнем моря отображаются на карте соответствующей линией — горизонталью.

В символических (знаковых) моделях представление величин и отношений между ними осуществляется с помощью букв, чисел и других знаков. Основное преимущество этих моделей — «вариантность». Одним знаковым описанием кодируются физически различные системы. Большое число конкретных значений параметров системы и, соответственно, число вариантов её поведения могут быть изучены на одной и той же
модели.

При исследовании объекта могут быть использованы все четыре типа моделей. Вербальные и изобразительные модели при этом могут рассматриваться в качестве инструмента первого приближения решения задачи.

Возможны комбинации различных типов моделей. Так, в тренажёры включают и аналоговые и знаковые блоки.

3) В зависимости от способа отображения объекта различают модели аналитические и имитационные.

В аналитических моделях используются полученные из различных соображений зависимости между выходными и входными переменными модели, в том числе, при необходимости, зависимости для вычисления критериальной функции. При этом для заданных входных возмущений обеспечивается вычисление исходов модели без имитации реальных процессов, протекающих в объекте. Для аналитических моделей наиболее характерны вербальные и знаковые способы описания.

Имитационная модель имитирует исследуемый объект, течение реального процесса. Для имитационных моделей используются все способы описания.

Термин «реальный процесс» здесь и далее используется в смысле процесс «существующей» или «способный принять форму существования». Это равным образом относится к аналитическим и имитационным моделям.

Выбор между аналитической и имитационной моделями определяется задачами исследования, уровнем знаний об объекте и квалификацией исследователя.

Для лучшего уяснения разницы между аналитическими и имитационными моделями рассмотрим пример моделирования случайного блуждания частицы по целочисленным точкам действительной прямой, при котором на каждом шаге частица с вероятностью p смещается по числовой оси на +1 и с вероятностью q = 1-p — на –1.

Пусть i —начальное положение частицы, j — положение частицы через n-шагов,

n = 0,1,2,..., P_n (i ®j) — вероятность перехода частицы за n-шагов из состояния i в состояние j.

Попасть из i в j возможно, если в направлении от i к j сделано m из n шагов, где m =(n + |j-i|)/2 должно быть целым, т.е. разность |j-i| должна иметь ту же четность, что и n.Естественно, переход из состояния i в состояние j не возможен, если n < |j-i|.

Вероятность перехода из i в j будет зависеть от двух величин m и n.

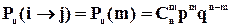
Таким образом, построена аналитическая модель (распределение вероятностей), с помощью которой можно получить вероятность нахождения частицы через n-шагов в любом j-ом состоянии, если начальное i-ое состояние частицы известно.

При имитационном моделировании, чтобы получить искомую вероятность, потребуется провести серию из N испытаний. При каждом отдельном испытании моделируется движение частицы длительностью в n шагов, начиная с i-го начального состояния. При этом, для определения направления движения частицы на каждом шаге разыгрывается случайная величина, принимающая значение +1 или –1 с заданными вероятностями. При каждом испытании записывается, где оказалась частица после
n-шагов.

Пусть после N испытаний, каждое из которых состояло из n-шагов, частица K-раз оказалась в состоянии j. Тогда P_n(i ®j) = K / N.