Требование замкнутости модели.

Если известно начальное состояние системы и известны на некотором интервале внешние воздействия и управления, то модель объекта должна позволить определить на этом интервале все переменные, характеризующие состояние объекта.

4) Требование устойчивости.

Модель должна быть устойчива (вычислительный процесс не должен расходиться) для тех условий и возмущений, для которых устойчив моделируемый объект. Следует отметить, что существует много показателей устойчивости.

Устойчивость модели (сходимость метода) в каждом конкретном случае связана с определенными условиями. Например, иногда при включении в модель аналоговой ЭВМ неустойчивость возникает вследствие собственных « люфтов « ЭВМ. И при использовании в модели цифровой ЭВМ неустойчивость может, вследствие особенностей вычислительного процесса, появится там, где в моделируемом непрерывном процессе устойчивость гарантирована.

5) Требование аддитивности.

Должна быть предусмотрена возможность уточнения структуры модели и обновления модельной информации.

Требование удобства.

Вся используемая в модели информация, в том числе все промежуточные и конечные результаты должны представляться оперативно в удобной форме. Соответственно, в модель должен быть включен набор средств, способствующих плодотворному взаимодействию человека и модели, в том числе сервисные программы, обеспечивающие простоту и удобство использования модели.

Структура моделей

В самом общем виде модель может быть представлена в виде схемы, показанной на рис. 2.

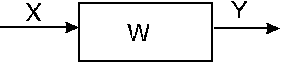
Рис.2.

На рис. 2:

X — вектор входных (экзогенных) переменных;

Y — вектор выходных переменных — исходы модели;

W — оператор модели, обеспечивающий преобразование входной информации в выходную в соответствие с задачей, решаемой на модели.

Также в общем случае в состав модели входят:

- компоненты;

- параметры;

- переменные;

- функциональные зависимости;

- ограничения;

- целевая (критериальная) функция.

Под компонентами модели реальной системы (объекта) понимаются модели отдельных элементов (подсистем) моделируемой системы (объекта).

Параметры после их определения и ввода в модель являются постоянными величинами. Некоторые параметры могут быть переменными. Определение значений параметров модели может рассматриваться как самостоятельная задача.

Переменные величины модели делятся на экзогенные и эндогенные. Экзогенные переменные (внешние по отношению к модели, «входные») являются следствием воздействия на систему окружающей среды или управлений. Эндогенные переменные характеризуют процессы, протекающие в модели. В каждый момент времени они либо характеризуют состояние модели — такие переменные также называются фазовыми координатами, либо определяют исходы, генерируемые моделью, — такие эндогенные переменные называются выходными или исходами системы.

Следует также различать управляемые и неуправляемые переменные.

W — оператор системы, определяет функциональные соотношения между переменными модели.

Ограничения устанавливают пределы изменения переменных, а также и допустимые пределы расхода ресурсов и средств на решение задачи, в том числе на время, которое можно использовать на исследование, чтобы получить результат к требуемому моменту. Ограничения могут быть искусственными — устанавливаются разработчиком модели или естественными – являются следствием свойств, присущих системе и окружающей среде.

Целевые (критериальные) функция (функционалы, отношения предпочтения) отражают цели исследования и содержат правила вычисления соответствующих критериев.

Возможны следующие варианты задач, решаемых на модели.

1) Прямая задача: известны Х и W, необходимо найти Y.

2) Обратная задача 1: известны Y и W, найти X.

3) Обратная задача 2: известны X и Y, найти W.

В задаче 1 в состав модели может включаться реальная система или ее подсистемы. Для обратной задачи 2 возможны два варианта: (1) анализ структуры оператора системы, (2) поиск оператора, обеспечивающего требуемое преобразование входной информации. В обратной задаче 2 при умелом подборе входной информации по анализу реакции системы на входное возмущение вскрывается структура системы. Здесь возможны случаи «черного ящика» — оператор системы полностью не известен, и «серого ящика» — структура известна, не известны значения параметров. Обратная задача может быть задачей синтеза. Поиск оператора для получения требуемого преобразования входного сигнала обеспечивается специальными оптимизирующими процедурами, реализуемыми в моделях.