Среднее арифметическое

Среднее арифметическое, или просто среднее, — одна из основных характеристик выборки.

Среднее арифметическое – такое значение признака, сумма отклонений от которого выборочных значений признака равна нулю (с учетом знака отклонения).

Среднее принято обозначать той же буквой, что и варианты выборки, с той лишь разницей, что над буквой ставится символ усреднения — черта. Например, если обозначить исследуемый признак через X, а его числовые значения — через x_i, то среднее арифметическое имеет обозначение .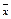

Среднее арифметическое, как и другие числовые характеристики выборки, может вычисляться как по необработанным первичным данным, так и по результатам группировки этих данных.

Для несгруппированных данных среднее арифметическое определяется по следующей формуле:

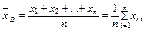
где n — объем выборки;

х_i — варианты выборки.

Если данные сгруппированы, то

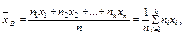
где n — объем выборки;

k — число интервалов группировки;

n_i — частота i-ого интервала;

х_i — срединное значение i-ого интервала.

Среднее арифметическое – величина того же наименования, что и значения признаков.

Нахождение среднего арифметического непрерывного вариационного ряда осложняется, если крайние интервалы не замкнуты (то есть имеют вид «менее 10» или «более 60»). В этом случае считается, что ширина первого интервала равна ширине второго, а ширина последнего – ширине предпоследнего.

Среднее арифметическое, вычисленное по формуле называют также взвешенным средним, подчеркивая этим, что в формуле x_i, суммируются с коэффициентами (весами), равными частотам попадания в интервалы группировки.

Медиана

Медианой (Ме) называется такое значение признака X, когда ровно половина значений экспериментальных данных меньше ее, а вторая половина — больше.

Если данных немного (объем выборки невелик), медиана вычисляется очень просто. Для этого выборку ранжируют, т. е. располагают данные в порядке возрастания или убывания, и в ранжированной выборке, содержащей n членов, ранг R (порядковый номер) медианы определяется как

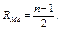
Пример 7.8. Имеется ранжированная выборка, содержащая нечетное число членов n = 9:

12, 14, 14, 18, 20, 22, 22, 26, 28.

Тогда ранг медианы:

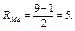
и медиана совпадает с пятым членом ряда: Ме = 20.

Если выборка содержит четное число членов, то медиана не может быть определена столь однозначно.

Пример 7.9. Имеется ранжированная выборка, содержащая 10 членов:

6, 8, 10, 12, 14, 16, 18, 20, 22, 24.

Ранг медианы оказывается равным:

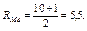
Медианой в этом случае может быть любое число между 14 и 16 (5-м и 6-м членами ряда). Для определенности принято считать в качестве медианы среднее арифметическое этих значений, т. е.:

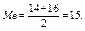
Если необходимо найти медиану для сгруппированных данных, то поступают следующим образом. Вначале находят интервал группировки, в котором содержится медиана, путем подсчета накопленных частот или накопленных относительных частот.

Медианным будет тот интервал, в котором накопленная частота впервые окажется больше 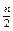или накопленная относительная частота — больше 0,5. Внутри медианного интервала медиана определяется по следующей формуле:

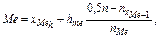
где 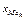— нижняя граница медианного интервала;

h_me — ширина медианного интервала;

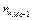— накопленная частота интервала, предшествующего медианному,

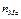— частота медианного интервала.

Пример 7.10. Найти медиану для интервального ряда примера 6.3.

Объем выборки равен п = 50 + 32 + 26 + 11 + 5 = 124.

Найдем медианный интервал – интервал, в котором накопленная частота впервые окажется больше 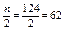или накопленная относительная частота — больше 0,5.

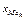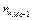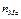Так как, накопительная частота второго интервала 50 + 32 = 82 > 62, то следовательно интервал (30; 40) будет медианным и = 30, h_me = 40 – 30 = 10, = 50, = 32.

Значит,

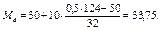
Медиана обычно несколько отличается от среднего арифметического. Так бывает всегда, когда имеет место несимметричная форма эмпирического распределения.

Мода

Мода (Мо) представляет собой значение признака, встречающееся в выборке наиболее часто.

Ряд называется унимодальным, если в нем только одно модальное значение и полимодальным, если есть несколько значений признака, которые встречаются одинаково часто. Для полимодального ряда моду не вычисляют.

Для дискретного ряда мода находится по определению.

Интервал группировки с наибольшей частотой называется модальным.

Для определения моды в интервальном ряду используется следующая формула:

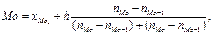
где 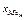— нижняя граница модального интервала;

h — ширина интервала группировки;

n_Mo — частота модального интервала;

n_Mo-1 — частота интервала, предшествующего модальному;

n_Mo+1 — частота интервала, следующего за модальным.