Коэффициент осцилляции
С целью, аналогичной введению коэффициента вариации, вводитсякоэффициент осцилляции по формуле:
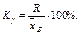
Литература:
Гмурман, В. Е. Теория вероятностей и математическая статистика: Учеб. пособие для вузов/В. Е. Гмурман. — 9-е изд., стер. — М.: Высш. шк., 2003. — с.187 – 197.
Контрольные вопросы:
1. Каково назначение математической статистки?
2. На какие области подразделятся математическая статистика?
3. Что называют генеральной совокупностью, выборочной совокупностью?
4. Какие виды выборок вы знаете? Дайте им определение. Приведите примеры.
5. Какие способы отбора применяются при формировании выборки?
6. Что представляют собой вариационные ряды? Каких типов они бывают? Приведите примеры.
7. Что представляют собой гистограмма и полигон частот?
8. Что представляет собой эмпирическая функция распределении? Какими свойствами она владеет?
9. Перечислите числовые характеристики выборки. Дайте им определения и методику их расчета.
Задания для самостоятельного решения
Задание 7.1. Выборка задана в виде распределения частот:
| X | ||||
| ni |
Найти распределение относительных частот. Найти эмпирическую функцию. Построить полигон частот и гистограмму.
Задание 7.2. Выборка сгруппированных данных случайной величины Х определена таблицей:
| X | |||||||
| ni |
Найти числовые характеристики выборки.
Задание 7.3. Выборка сгруппированных данных случайной величины Х определена таблицей:
| X | 10-20 | 21-30 | 31-40 | 41-50 | 51-60 | 61-70 | 71-80 |
| ni |
Найти числовые характеристики выборки, эмпирическую функцию. Построить полигон частот, гистограмму и график эмпирической функции.
Тема 8
Теория оценок
8.1. Статистические оценки параметров распределения.
8.2.Несмещенные, эффективные и состоятельные оценки.
8.3. Точность оценки, доверительная вероятность (надежность). Доверительный интервал.
8.1. Статистические оценки параметров распределения
Пусть требуется изучить количественный признак генеральной совокупности. Допустим, что из теоретических соображений удалось установить, какое именно распределение имеет признак. Естественно возникает задача оценки параметров, которыми определяется это распределение.
Например, если наперед известно, что изучаемый признак распределен в генеральной совокупности нормально, то необходимо оценить (приближенно найти) математическое ожидание и среднее квадратическое отклонение, так как эти два параметра полностью определяют нормальное распределение; если же есть основания считать, что признак имеет, например, распределение Пуассона, то необходимо оценить параметр X, которым это распределение определяется.
Обычно в распоряжении исследователя имеются лишь данные выборки. Через эти данные и выражают оцениваемый параметр.
Рассматривая x1, x2, .. ., хп как независимые случайные величины x1, x2, .. ., хп, можно сказать, что найти статистическую оценку неизвестного параметра теоретического распределения — это значит найти функцию от наблюдаемых случайных величин, которая и дает приближенное значение оцениваемого параметра.
Итак, статистической оценкой неизвестного параметра теоретического распределения называют функцию от наблюдаемых случайных величин.
Дата добавления: 2016-07-27; просмотров: 2724;











