Классическая вероятность и ее свойства

Вероятность — одно из основных понятий теории вероятностей. Существует несколько определений этого понятия. Приведем определение, которое называют классическим.

Вероятностью события называется отношение числа элементарных исходов, благоприятствующих данному событию, к числу всех равновозможных исходов опыта, в котором может появиться это событие.

Вероятность события А обозначают через Р(А) (здесь Р – первая буква французского слова probabilite – вероятность).

В соответствии с определением

,

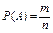где 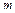– число элементарных исходов испытания, благоприятствующих появлению события ;

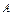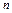- общее число возможных элементарных исходов испытания.

Это определение вероятности называют классическим. Оно возникло на начальном этапе развития теории вероятностей.

Часто число 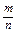называют относительной частотой появления события А в опыте.

Чем больше вероятность события, тем чаще оно наступает, и наоборот, чем меньше вероятность события, тем реже оно наступает. Когда вероятность события близка к единице или равна единице, то оно наступает почти при всех испытаниях. О таком событии говорят, что оно практически достоверно, т. е. что можно наверняка рассчитывать на его наступление.

Наоборот, когда вероятность равна нулю или очень мала, то событие наступает крайне редко; о таком событии говорят, что оно практически невозможно.

Иногда вероятность выражают в процентах: Р(А) • 100% есть средний процент числа появлений события A.

Пример 2.13. Набирая номер телефона, абонент забыл одну цифру и набрал ее наудачу. Найти вероятность того, что набрана нужная цифра.

Решение.

Обозначим через А событие — «набрана нужная цифра».

Абонент мог набрать любую из 10 цифр, поэтому общее число возможных элементарных исходов равно 10. Эти исходы несовместны, равновозможны и образуют полную группу. Благоприятствует событию А лишь один исход (нужная цифра лишь одна).

Искомая вероятность равна отношению числа исходов, благоприятствующих событию, к числу всех элементарных исходов:

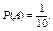
Формула классической вероятности дает очень простой, не требующий проведения экспериментов, способ вычисления вероятностей. Однако простота этой формулы очень обманчива. Дело в том, что при ее использовании возникают, как правило, два очень непростых вопроса:

1. Как выбрать систему исходов опыта так, чтобы они были равновозможны, и можно ли это сделать вообще?

2. Как найти числа m и n?

Если в опыте участвуют несколько предметов, равновозможные исходы увидеть не всегда просто.

Великий французский философ и математик Даламбер вошел в историю теории вероятностей со своей знаменитой ошибкой, суть которой в том, что он неверно определил равновозможность исходов в опыте всего с двумя монетами!

Пример 2.14. (ошибка Даламбера). Подбрасываются две одинаковые монеты. Какова вероятность того, что они упадут на одну и ту же сторону?

Решение Даламбера.

Опыт имеет три равновозможных исхода:

1. Обе монеты упадут на «орла»;

2. Обе монеты упадут на «решку»;

3. Одна из монет упадет на «орла», другая на «решку».

Из них благоприятными для нашего события будут два исхода, поэтому искомая вероятность равна .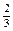

Правильное решение.

Опыт имеет четыре равновозможных исхода:

1. Первая монета упадет на «орла», вторая тоже на «орла»;

2. Первая монета упадет на «решку», вторая тоже на «решку»;

3. Первая монета упадет на «орла», а вторая — на «решку»;

4. Первая монета упадет на «решку», а вторая — на «орла».

Из них благоприятными для нашего события будут два исхода, поэтому искомая вероятность равна .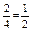

Даламбер совершил одну из самых распространенных ошибок, допускаемую при вычислении вероятности: он объединил два элементарных исхода в один, тем самым сделав его не равным по вероятности оставшимся исходам опыта.