Геометрическое определение вероятности

В предыдущем пункте мы научились вычислять вероятности событий в опытах, имеющих конечное число равновозможных исходов. Для этого не требуется проводить никаких экспериментов — нужно всего лишь правильно посчитать количество всех возможных исходов опыта и количество исходов, благоприятных для данного события. А как быть, если этих исходов бесконечно много? Посмотрим, как все же и в этом случае вычислить вероятность без обращения к опыту.

Выберем на географической карте мира случайную точку. Какова вероятность, что эта точка окажется в Белоруссии? Очевидно, для ответа на вопрос нужно знать, какую часть всей карты занимает Белоруссия. Точнее, какую часть всей площади карты составляет площадь Белоруссии. Отношение этих площадей и даст искомую вероятность.

Такую же картину мы имеем и в общем случае, когда в некоторой ограниченной области Ω 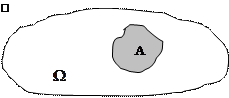случайно выбирается точка:

Если предположить, что попадание в любую точку области Ω равновозможно, то вероятность попадания случайной точки в заданное множество A будет равна отношению площадей:

.

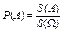(через P мы, как и раньше, обозначаем вероятность, а через S — площадь).

Такое определение вероятности называется геометрическим. Ситуация напоминает классическое определение вероятности: как и там, здесь важна равновозможность всех исходов, т.е. всех точек области. Но теперь число исходов эксперимента бесконечно, поэтому приходится считать не их количество, а занимаемую ими площадь.

Пример 2.15. В круг вписан квадрат. В круг наудачу бросается точка. Какова вероятность того, что точка попадает в квадрат?

Решение:

Введем обозначения:

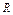– радиус круга, а – сторона вписанного квадрата, событие А – «попадание точки в квадрат».

Известно, площадь круга 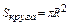. Сторона вписанного квадрата через радиус описанной окружности выражается формулой 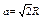, поэтому площадь квадрата .

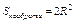Следовательно,

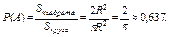
Точно так же можно определить геометрическую вероятность в пространстве (вместо площадей здесь надо брать объемы тел) и на прямой (а здесь — длины отрезков).