Алгоритм решения задач на классическую вероятность:

1. Описание возможных исходов опыта, их кодирование и перечисление (полное или частичное).

2. Обоснование равновозможности перечисленных исходов (здесь можно опираться на симметрию самого объекта, участвующего в опыте; использовать прямые указания в тексте задачи: «случайно», «наугад», «не глядя» и т.д.).

3. Подсчет общего числа исходов опыта n.

4. Описание благоприятных для события A исходов, их перечисление (полное или частичное). Если все исходы уже выписаны, то можно просто отметить среди них благоприятные для A.

5. Подсчет числа благоприятных для события A исходов m.

6. Вычисление вероятности по формуле .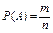

7. Оценка и интерпретация полученного результата.

Вероятность события имеет следующие свойства:

1. Для любого события А справедливо неравенство:

0 £ P(A) £ 1.

2. Вероятность невозможного события равна нулю.

3. Вероятность достоверного события равна единице.

4. Если события 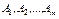образуют полную группу событий, то вероятность объединения этих событий равна единице:

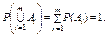
5. Вероятность противоположного события: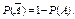

6. Если событие 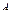влечет за собой событие 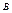, то вероятность события 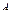не превосходит вероятность события 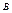, т.е.

<3 4 567 8 9 >

Дата добавления: 2016-07-27; просмотров: 2520;

Поиск по сайту

Узнать еще