УСЛОВИЕ ПЛАСТИЧНОСТИ И НАСТУПЛЕНИЕ
ПЛАСТИЧЕСКОГО СОСТОЯНИЯ
Энергетическое условие пластичности ортотропной среды можно представить следующим образом:
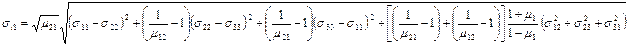
Здесь 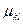 – коэффициенты поперечной деформации, где первый индекс показывает направление поперечной деформации, а второй – действие силы;
– коэффициенты поперечной деформации, где первый индекс показывает направление поперечной деформации, а второй – действие силы;
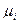 – коэффициент поперечной деформации, когда сила действует под углом 45º к осям 1 и 2 и т.д.;
– коэффициент поперечной деформации, когда сила действует под углом 45º к осям 1 и 2 и т.д.;
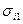 – интенсивность напряжений, отнесенная к оси 1.
– интенсивность напряжений, отнесенная к оси 1.
Наблюдаются следующие зависимости:
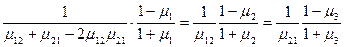 ,
,
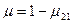 ,
, 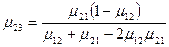 ,
,
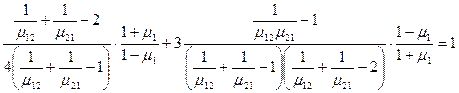 .
.
При плоской деформации 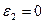 ,
, 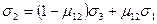 .
.
Для трансверсального изотропного тела (плоскость изотропии 1-2) условие пластичности можно записать в виде
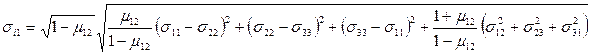 .
.
Наконец, при изотропном материале
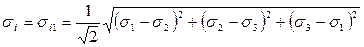 .
.
Условие пластичности Треска-Сен-Венана для изотропного материала:
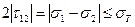 ,
,
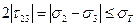 ,
,
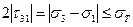 .
.
Задачи
10.1 Записать условие пластичности ортотропной среды для случая плоского напряженного и плоского деформированного состояния, используя выражение 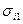 .
.
10.2 Произвести те же действия, что и в задаче 10.1, для трансверсального изотропного тела.
10.3 Энергетическое условие пластичности изотропного тела, записанное в главных осях, разрешить относительно 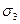 . Затем, используя данные табл. 10 и принимая условно у всех сплавов
. Затем, используя данные табл. 10 и принимая условно у всех сплавов 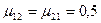 , определить, какие сжимающие или растягивающие напряжения
, определить, какие сжимающие или растягивающие напряжения 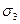 необходимо приложить, чтобы материал перешел в пластическое состояние.
необходимо приложить, чтобы материал перешел в пластическое состояние.
Таблица 10
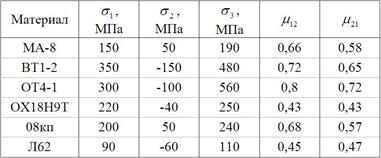
10.4 Аналогично 10.3 рассмотреть трансверсально-изотропное тело, считая плоскостью изотропии плоскость 1-2. В данных таблицы значение 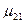 условно принять равным
условно принять равным  .
.
По результатам решения 10.2, 10.3 и 10.4 оценить влияние анизотропии.
10.5 В некоторой точке тела материал испытывает напряженное состояние, при котором 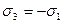 (
( 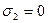 ). Исходя из энергетического условия пластичности, определить, при каких числовых значениях тело перейдет в пластическое состояние.
). Исходя из энергетического условия пластичности, определить, при каких числовых значениях тело перейдет в пластическое состояние.
Рассмотреть три случая:
а) среда изотропная 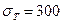 МПа;
МПа;
б) сплав трансверсально-изотропный (например, ОХ18Н9Т);
в) сплав ортотропный (например, МА-8).
10.6 Стальной изотропный толстостенный цилиндр находится под действием внутреннего давления 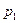 . Найти его величину из условия, что в металле впервые появилось пластическое состояние.
. Найти его величину из условия, что в металле впервые появилось пластическое состояние.
Используя выведенную формулу, определить значение 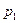 , если
, если 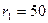 мм,
мм, 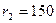 мм, а
мм, а 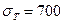 МПа.
МПа.
10.7 В случае цилиндрической анизотропии напряжения в толстостенных цилиндрах рассчитываются по формулам
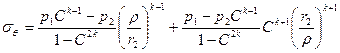 ,
,
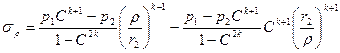 ,
,
где
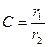 ,
, 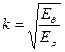 .
.
Принимая для стали 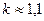 и используя условие пластичности в виде
и используя условие пластичности в виде
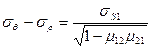 ,
,
где 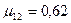 ,
, 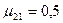 ,получить величины, заданные в 10.7.
,получить величины, заданные в 10.7.
10.8 В 10.6 принять, что действует не только внутреннее, но и наружное давление:
а) 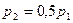 ;
;
б) 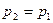 .
.
Что произойдет с цилиндром, если 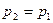 ?
?
10.9 Напряженное состояние в точке тела задано в виде тензора
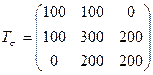 .
.
Принимая 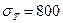 МПа, выяснить, в упругом или пластическом состоянии находится точка изотропной среды.
МПа, выяснить, в упругом или пластическом состоянии находится точка изотропной среды.
10.10 Напряжения в некоторой точке изотропного тела: 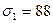 МПа,
МПа, 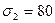 МПа,
МПа, 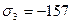 МПа. Может ли металл с пределом текучести
МПа. Может ли металл с пределом текучести 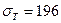 МПа находиться в упругом состоянии?
МПа находиться в упругом состоянии?
10.11 Напряжения в данной точке изотропного тела: 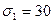 МПа,
МПа, 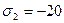 МПа,
МПа, 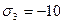 МПа. Каким пределом текучести должен обладать металл, чтобы при заданных напряжениях находиться в упругом состоянии?
МПа. Каким пределом текучести должен обладать металл, чтобы при заданных напряжениях находиться в упругом состоянии?
10.12 Под действием напряжений 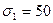 МПа,
МПа, 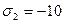 МПа,
МПа, 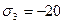 МПа изотропный металл согласно условию максимальных касательных напряжений оказался на пределе текучести. Какова величина предела текучести?
МПа изотропный металл согласно условию максимальных касательных напряжений оказался на пределе текучести. Какова величина предела текучести?
10.13 Записать условие пластичности максимальных касательных напряжений для плоского напряженного состояния ( 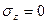 ) и дать его геометрическую интерпретацию.
) и дать его геометрическую интерпретацию.
10.14 Записать энергетическое условие пластичности для случая плоского напряженного состояния ( 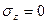 ) и дать его геометрическую интерпретацию.
) и дать его геометрическую интерпретацию.
Дата добавления: 2016-07-27; просмотров: 1637;











