К вычислению коэффициента корреляции между продолжительностью вегетации и массой 1000 семян ячменя

<11 12 131415 16 17 >

Вегетационный период, дни, х
Масса 1000 семян, г у	57,5-62,4	62,5-67,4	67,5-72,4	72,5-77,4	77,5-82,4	82,5-87,4	87,5-92,5	а_у	_fy	a_yf_y	a²_yf_y
				75=A_X
55-61 58		-6	-6					+3	₁₄
49-54,9 52		-20	-16					+2	₃₈
43-48,9 46		-14	-10					+1	₇₁
37-42,9 40=A_y									₅₈
31-36,9 34					-5	-2		-1	₂₆	-26
25-30,9 28								-2	₆	-12
19-24,9 22								-3	₁	-3
a_x	-3	-2	-1		+1	+2	+3			∑=	∑=408

f_x				N=	₂₁₄
a_xf_x	-6	-58	-34	∑=4
a²_xf_x				∑=310
f_xya_xa_y		-14	-27	∑= 66

Вычисления производим в следующем порядке:

1. Варианты по обоим признакам разбиваются на классы и производится разноска вариант совместно обоих рядов по клеткам корреляционной решетки. Аргумент (х) располагается в горизонтальном ряду таблицы слева направо. Значения функции (у) возрастают снизу вверх.

2. Вычисляется эмпирическая линия регрессии для выяснения степени криволинейности данной связи. Если эмпирическая линия регрессии близка к прямой линии и не является двускатной, можно вычислять коэффициент корреляции, в противном случае вычисляется показатель корреляции для криволинейных связей.

3. В корреляционной таблице произвольно выбирается условный центр. Обычно это близкая к центру клетка, содержащая наибольшую частоту (в нашем примере- клетка с частотой 20 вариант). В ряду х против нее находится условная средняя А_х=75, а в ряду у –А_у=40.

4. Вычисляем условные отклонения а_х: (60-75)/5 = -3; (65-75)/5= - 2; (70-75)/5 = - 1; (75-75) /5 = 0; (80-75)/5 =+1 и т.д.

Условные отклонения (а_х) записываем в горизонтальной строке.

5. Также вычисляем и условные отклонения а_у от условной средней А_у= 40. Условные отклонения записываем в вертикальной графе табл. 14.

6. Условные отклонения умножаем на соответствующие им частоты: а_хf_x = -3 x 2 = -6; -2 х 29 = - 58; -1 х 34 = -34 и т.д.; а_уf_у = +3 х 14 = 42; +2 х 38 = 76 и т.д.

7. Квадраты условных отклонений умножаем на их частоты: а²_хf_x = (-3)² х 2 = 18; (-2)² х 29 = 116; (-1)² х 34 =34 и т.д.

Аналогично проводим вычисления и для вариационного ряда у: a²_yf_y=3² x 14= 126; 2² x 38 =152 и т.д.

8. Находим произведения условных отклонений между собой и на имеющуюся совместную для них частоту. Вычисления начинаем по столбцам слева направо;

первый столбец: a_xa_yf_xy = (-3) x 0 x 1 =0; (-3) x 1 x (-1) =3;

второй столбец: (-2) х 3 х 1 = -6; (-2) х 2 х 5 = -20; (-2) х 1 х 7 = -14. Записываем результаты в правом верхнем углу соответствующих клеток табл. 14.

9. Суммируем совместные частоты по столбцам и записываем в горизонтальной строке снизу таблицы: 3; -14; -27; 0; 71; 18; 15.

10. Получаем суммы по строкам (ряд х) и по столбцам (ряд у):

∑f_x=N=214; ∑a_xf_x=4; ∑f_y=N=214; ∑a²_xf_x=310; ∑f_xya_xa_y= 66; ∑a_yf_y = 148; ∑a²_yf_y= 408.

11. Для проверки наших вычислений находим сигму ряда х и сигму ряда у по формулам:

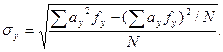
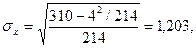
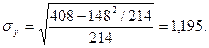
12. Подставляя вычисленные значения в формулу коэффициента корреляции, получаем:

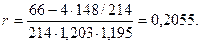
Для небольших групп вариационного ряда N < 100 ошибку коэффициента корреляции вычисляем по формуле m_z = , а для больших групп N > 100 - по формуле , где m_r- ошибка коэффициента корреляции; r – коэффициент корреляции; N- объем выборки (N > 100).

Для рассматриваемого примера m_r = (1- 0,2055²) / 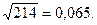критерий достоверности Стьюдента: Число степеней свободы при определении значимости коэффициента корреляции равно: 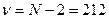. По таблице на доверительном уровне 95% он составляет 2,0.

Ввиду того, что вычисленное значение выше табличного, можно сделать заключение о имеющейся положительной небольшой, но достоверной зависимости между массой зерен ячменя и продолжительностью вегетации.

При расчете коэффициента корреляции на ЭВМ как для малых, так и для больших выборок Г.Н.Зайцев рекомендует формулу:

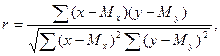где r – коэффициент корреляции; x – M _x – отклонения значений ряда аргумента от его средней; у - М _у- отклонения значений ряда функции от ее средней величины.