Вегетация в днях и масса 1000 семян в г у 214 сортов ячменя
| Масса 1000 семян (у) | Продолжительность вегетации (х) |
| Границы | класса | 57,5-62,4 | 62,5-67,4 | 67,5-72,4 | 72,5-77,4 | 77,5-82,4 | 82,5-87,4 | 87,5-87,4 | fy | х/у |
| Середина | класса | |||||||||
| 55-61 | 76,8 | |||||||||
| 49-54,9 | 75,4 | |||||||||
| 43-48,9 | 76,3 | |||||||||
| 37-42,9 | 74,6 | |||||||||
| 31-36,9 | 73,3 | |||||||||
| 25-30,9 | 70,0 | |||||||||
| 19-24,9 | 65,0 | |||||||||
| fx | N=214 | |||||||||
| у/х | 37,0 | 41,4 | 44,8 | 42,9 | 45,8 | 46,8 | 47,5 |
Исходные данные разносятся по классам корреляционной решетки так же, как и при составлении отдельного взвешенного вариационного ряда с той лишь разницей, что в данном случае каждая точка в клетке корреляционной решетки (частота) соответствует значениям обоих рядов. При этом сумма частот столбцов должна равняться сумме частот строк, в нашем примере N=214.
3. Расчет эмпирической линии регрессии у/х, которая используется при вычислении прямого корреляционного отношения, ведется путем определения взвешенных средних арифметических для отдельных участков ряда у или групп вариант, имеющих частоты. Например, точка 37,0 вычислена следующим образом: 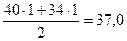 .
.
4.Эмпирическая линия регрессии х/у вычисляется в том случае, если требуется определить обратное корреляционное отношение, т.е. когда правильность первоначального назначения аргумента вызывает сомнение. Точки х/у получаем путем определения групповых средних в горизонтальных рядах корреляционной решетки. Например:
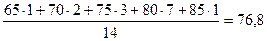 .
.
5. Вычисленные точки эмпирической линии регрессии у/х наносятся на график и соединяются линией, что позволяет судить о имеющейся связи между изучаемыми признаками. В нашем случае связь положительная, так как при возрастании аргумента функция возрастает и (если построить кривую) близка к прямолинейной. Следовательно, в нашем случае для выявления силы связи можно будет применить коэффициент корреляции.
При обработке малых вариационных рядов корреляционная решетка не составляется, однако график зависимости у от х вычерчивается для выявления существующей формы взаимосвязи.
Дата добавления: 2020-10-25; просмотров: 610;











