Зависимость урожая сои от высоты растений
(к вычислению коэффициента корреляции с преобразованием имеющихся данных)
| ах = х - Ах | ау = у – Ау | ах2 | ау2 | ахау |
| -2 | -4 | Ё4 | +8 | |
| -1 | -9 | +9 | ||
| +9 | -3 | -27 |
Продолжение табл. 13
| +18 | +21 | +378 | ||
| +2 | -22 | -44 | ||
| -20 | -21 | +420 | ||
| -21 | +14 | -294 | ||
| -10 | +14 | -140 | ||
| -1 | +4 | -4 | ||
| +10 | +13 | +130 | ||
| +10 | +2 | +20 | ||
| -3 | ||||
| +13 | -11 | -143 |
Суммы столбцов
| +7 | -5 |
Проверим результаты вычислений :
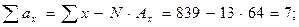
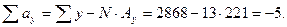 Найденные суммы подставляем в формулу:
Найденные суммы подставляем в формулу: 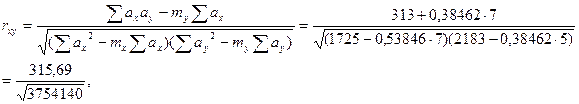
где 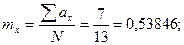
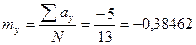
Под знаком радикала получилось большое число, которое можно уменьшить, представив его в виде произведения с 10 в четной степени:
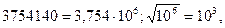 следовательно (после сокращения на 103) = 1000:
следовательно (после сокращения на 103) = 1000: 
Оценка достоверности коэффициента корреляции производится путем преобразования его при помощи таблицы, приведенной в приложении (приложение, табл. 4). Из таблицы берем z = 0,33 для r = 0,32. Ошибка вычисляется по формуле:
mz = 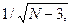 где mz - ошибка преобразованного коэффициента корреляции; N- объем выборки. Для рассматриваемого примера
где mz - ошибка преобразованного коэффициента корреляции; N- объем выборки. Для рассматриваемого примера  Критерий достоверности Стьюдента будет: t=z / mz = 0,33 / 0,32 = 1,03. Как видим, вычисленное значение критерия достоверности меньше табличного, которое на уровне 0,95 равно 2,2. Число степеней свободы при оценке преобразованного коэффициента корреляции принимается:
Критерий достоверности Стьюдента будет: t=z / mz = 0,33 / 0,32 = 1,03. Как видим, вычисленное значение критерия достоверности меньше табличного, которое на уровне 0,95 равно 2,2. Число степеней свободы при оценке преобразованного коэффициента корреляции принимается:  В нашем примере коэффициент корреляции оказался не достоверным, что могло произойти или в результате недостаточного количества вариант в выборке, или в результате отсутствия исследуемой связи в изучаемой совокупности. Следует отметить, что достоверность коэффициента корреляции (r) можно оценить, не обращаясь к таблице по формуле:
В нашем примере коэффициент корреляции оказался не достоверным, что могло произойти или в результате недостаточного количества вариант в выборке, или в результате отсутствия исследуемой связи в изучаемой совокупности. Следует отметить, что достоверность коэффициента корреляции (r) можно оценить, не обращаясь к таблице по формуле: 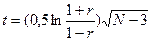 , где N - объем выборки, t - критерий Стьюдента, при числе степеней свободы
, где N - объем выборки, t - критерий Стьюдента, при числе степеней свободы 
.
Дата добавления: 2020-10-25; просмотров: 630;











