Корреляционного отношения

Метод может быть применен тогда, когда при наличии больших вариационных рядов требуется количественно определить не только силу связи между признаками, но и степень ее криволинейности, если требуется получить представление о знаке данной зависимости. Квадрат коэффициента корреляции, часто называют коэффициентом детерминации. Данный метод дает возможность вычислить точки эмпирической линии регрессии у/х, для построения графика изучаемой связи.

Вычисление квадратов коэффициента корреляции и прямого корреляционного отношения по совмещенному алгоритму ведется по формулам: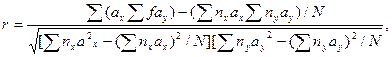

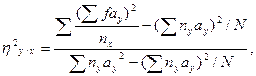где r – коэффициент корреляции; а_х - условные отклонения вариант ряда х от начала ряда; f- частоты корреляционной решетки; а_у- условные отклонения вариант ряда у от начала ряда; n_x – суммы частот по столбцам корреляционной решетки; n_y - суммы частот по строкам корреляционной решетки; N – объем выборки; 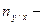прямое корреляционное отношение.

Последовательность вычислений по формулам:

1. Корреляционную решетку составляем таким образом, чтобы варианты ряда аргумента (х) располагались в верхней строке решетки слева направо, а варианты ряда функции (у) располагались бы в вертикальном столбце снизу вверх (табл. 15).

Таблица 15